Resolução de Problemas por Meio de Busca

Inteligência Artificial

Pontifícia Universidade Católica de Campinas

Prof. Dr. Denis M. L. Martins

Objetivos de Aprendizado

  • Compreender a formalização de problemas como busca em espaço de estados.
  • Analisar diferentes estratégias de busca não‑informada.

Recaptulando o modelo PEAS

  • Defina a tarefa: Determine quais são as metas do agente (ex.: “navegar pelo labirinto”).
  • Especifique P: Escolha métricas claras que quantifiquem sucesso (ex.: número de passos até o objetivo, tempo total, custo energético).
    • Medir progresso. Indicar caminho promissor.
  • Descreva E: Modele o ambiente em termos de estado inicial, transições e observabilidade.
    • Representar aspectos importantes do problema. Nem toda informação é relevante.
  • Determine A: Especifique quais ações podem ser executadas pelo agente para alterar o ambiente.
  • Liste S: Identifique quais percepções são necessárias para tomar decisões corretas.

Representação do Problema

  • Estado inicial
  • Conjunto de ações para cada estado .
  • Função sucessora .
  • Custo da ação .
  • Função meta ou conjunto de estados‑meta.
  • Objetivo: Estado final desejado.

  • Solução: sequência de ações que levam de um estado inicial a um estado objetivo.
  • Solução ótima: aquela que apresenta custo mínimo.

Buscar uma solução em um espaço (geralmente) grande de soluções.

Espaço de busca (de estados)

Espaço de Estados (ou de busca)

  • Conjunto completo de estados que podem ser alcançados a partir do estado inicial por meio da aplicação sucessiva das ações disponíveis.
  • Representação em grafo ou árvore.
  • Cada nó desta estrutura representa um estado possível e cada arco indica uma transição legal entre dois estados.

Exemplo 1: Navegação

  • Problema: Navegação de um robô num grid 4×4 com obstáculos.
  • Objetivo: Chegar em uma sala específica.
  • Estado inicial: (x=0, y=0).
  • Ações: Norte, Sul, Leste, Oeste (restritas por limites e obstáculos).
  • Sucessor: Result((x,y), Norte) → (x, y+1) se não houver obstáculo.
  • Espaço de busca: Conjunto de todas as coordenadas possíveis (i,j) tais que 0 ≤ i,j < 4 e sem obstáculos.

Tipos de tarefas de busca

  • Planejamento: O caminho que leva a solução é importante (e.g., labirinto, rota)
  • Identificação: Saber/Encontrar a solução é o importante (e.g., colorir um mapa)

Exemplo 2: Torre de Hanoi

Um puzzle de empilhamento de blocos.

  • Há 3 torres (, , ).
  • Discos de tamanhos distintos (1‑pequeno, 2‑médio, 3‑grande) são empilhados nas torres.
  • Regra: um disco nunca pode ser colocado sobre outro menor.

Exemplo 2: Torre de Hanoi (cont.)

Elemento Descrição
Estado inicial – todos os discos na torre  (do maior ao menor).
Conjunto de ações Mover o disco superior da torre para a torre , onde e a ação é legal.
Função sucessora Remove o topo da torre origem e coloca sobre a torre destino, gerando novo estado.
Custo da ação 1 (todos os movimentos têm custo unitário).
Condição de meta Todos os discos na torre : .

O espaço de estados possui combinações possíveis,
mas apenas 15 são válidas quando se considera a regra de empilhamento.

Exemplo 2: Torre de Hanoi (cont.)

  1. Ação: Mover disco 1 da para → Estado
  2. Ação: Mover disco 2 da para → Estado
  3. Ação: Mover disco 1 da para → Estado
  4. Ação: Mover disco 3 da para → Estado
  5. Ação: Mover disco 1 da para → Estado
  6. Ação: Mover disco 2 da para → Estado
  7. Ação: Mover disco 1 da para → Estado (meta).

Exemplo 3: 8-Puzzle

  • O 8‑Puzzle é um quebra‑cabeça de lógica composto por nove peças quadradas, numeradas de 1 a 8, dispostas em um tabuleiro (). Uma das posições permanece vazia (na figura abaixo, cinza).
  • O objetivo do jogo é reordenar as peças até que o tabuleiro esteja na configuração desejada (na figura, com as peças em ordem crescente).

center
Fonte da imagem: https://8-puzzle.readthedocs.io/en/latest/

Exemplo 3: 8-Puzzle (cont.)

  • Espaço de estados: permutações possíveis.
  • Como podemos representar um estado?
  • Qual conjunto de ações permitidas?
  • Como avaliar o progresso e o sucesso?

center
Fonte da imagem: https://8-puzzle.readthedocs.io/en/latest/

Características importantes em problemas de busca

  • Completude: O algoritmo encontra uma solução, dado que ela exista?
  • Otimalidade: Quando o algoritmo encontra uma solução, ela é a melhor possível?
  • Complexidade de Tempo: Como o tempo de processamento do algoritmo se comporta em função do tamanho da entrada?
  • Complexidade de Espaço: Como o espaço ocupado pelas informações necessárias ao algoritmo se comporta em função do tamanho da entrada?

Buscando soluções (cont.)

  • Após a formulação do problema, precisamos buscar por uma solução.
  • Podemos aplicar algoritmos de busca que consideram várias sequências de ações possíveis.
    • Como navegar sistematicamente pelo espaço de busca?
    • Como representar este espaço?
  • Cuidado: Manter o mínimo de informação armazenada, o que muitas vezes implica em não gerar/armazenar todos os possíveis estados em memória.

Buscando soluções (cont.)

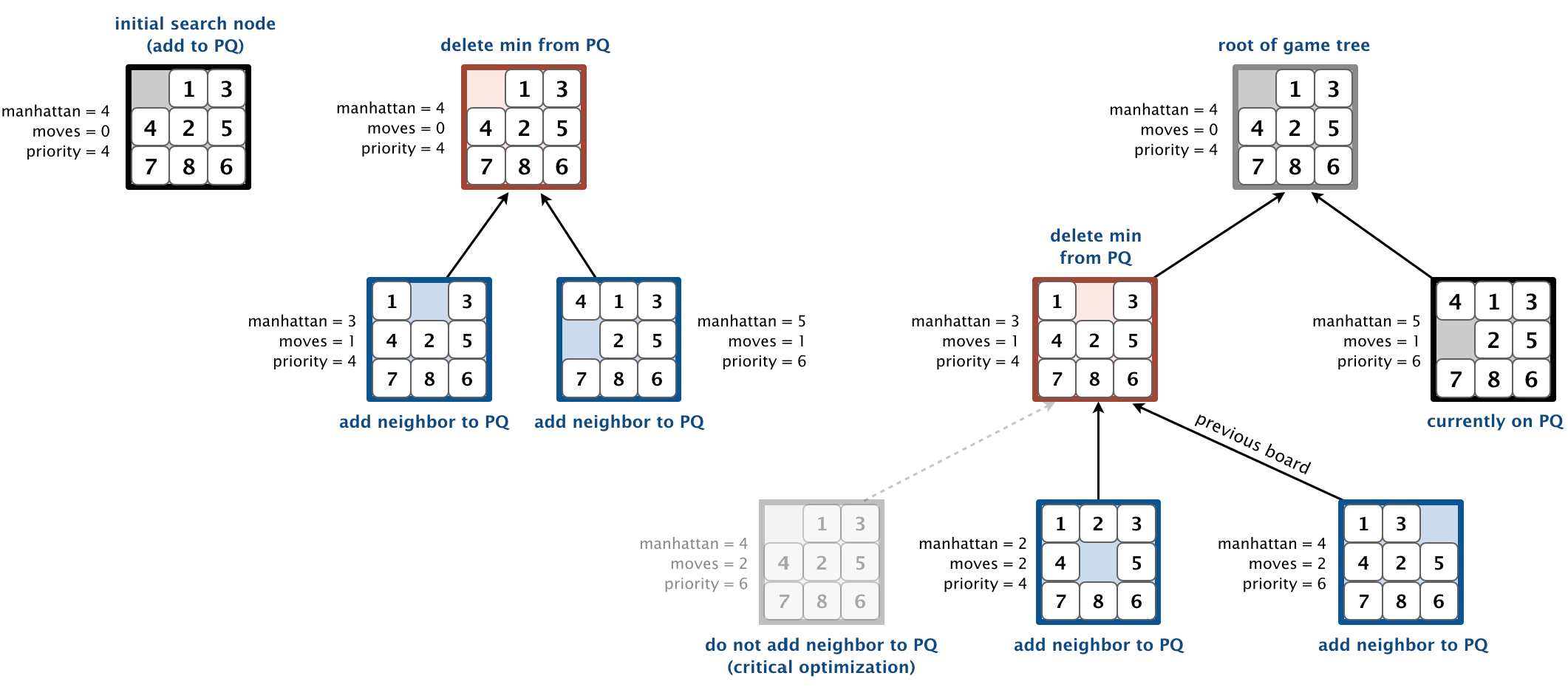
  • Os algoritmos começam de um estado inicial e as sequências de ações formam um árvore de busca:
    • Nó raiz representa o estado inicial.
    • Cada nó representa um estado e cada aresta a aplicação de uma ação.
  • A cada ação, a árvore de busca é expandida.
    • Fronteira: nós a seres expandidos.
    • Estratégia de expansão/busca: escolher o nó mais promissor a ser expandido.


Fonte da imagem: https://8-puzzle.readthedocs.io/en/latest/

Visão geral de um algoritmo de busca

Iteração Principal – enquanto a fronteira não estiver vazia:

  1. Seleção: retirar o nó mais promissor segundo a política de expansão.
  2. Teste de Meta: verificar se o estado extraído satisfaz a condição de objetivo; se sim, devolver caminho e terminar.
  3. Expansão: gerar sucessores aplicando todas as ações admissíveis ao estado atual, calculando custo e heurística de cada filho.
  4. Atualização: insere nós gerados na fronteira e volta para o passo 1
  • Convergência ou Terminação – algoritmo termina quando encontra meta, quando a fronteira esvazia (sem solução) ou quando excede limites pré‑estabelecidos (tempo/memória).

Estratégias de Busca Não‑Informada

Algoritmos que exploram o espaço de estados sem utilizar nenhuma informação adicional (heurística) sobre a distância até o objetivo que ajude a filtrar ações, sendo necessário buscar exaustivamente pelo espaço de estados.

Busca em Largura (BFS) – Nós são expandidos na ordem que foram criados. Usa fila. Expande níveis sucessivos; garante solução ótima em custo unitário.

Busca em Profundidade (DFS) – O último nó criado é o primeiro a ser expandido. Usa pilha. Não é completa. Não garante otimalidade.

Busca em Largura (BFS)

  • Todos os nós em dada profundidade na árvore de busca são expandidos, antes que todos os nós no nível seguinte sejam expandidos.
  • Estrutura de dados principal: fila FIFO (first‑in, first‑out).
  1. Inserir o nó inicial na fila.
  2. Repetir enquanto a fila não estiver vazia:
    a. Remover o primeiro nó n da fila.
    b. Se n é solução, retornar caminho até n.
    c. Expandir n, gerando todos os sucessores e inserindo-os na fila (apenas se ainda não foram visitados).

Busca em Largura (BFS)

Fonte: https://www.codecademy.com/article/bfs-vs-dfs

BFS: Completude e Otimalidade

  • Completeness: garante encontrar uma solução se existir, desde que a árvore seja finita.
  • Optimality: fornece caminho mínimo em árvores com custo uniforme (quando todos os custos de passos forem iguais). Não garante otimalidade quando custos variam.

BFS: Complexidade de tempo

  • Assuma uma árvore onde cada estado (nó) tem sucessores (nós filhos). sucessores.
    • A raiz da árvore de busca gera b nós no primeiro nível, cada um dos quais gera b outros nós, totalizando no segundo nível.
    • Cada nó do segundo nível gera mais outros nós, totalizando nós no terceiro nível...
  • Assumindo uma solução que esteja no nível de profundidade :
    • No pior caso, o número total de nós gerados é
    • Em notação Big O, temos .

BFS: Complexidade de espaço (memória)

  • Qualquer busca em grafos (ou árvores) que armazena todos os nós expandidos no conjunto explorado, a complexidade do espaço está sempre dentro de um fator de
    da complexidade do tempo.
  • Na BFS cada nó gerado permanecerá na memória. Ou seja, a fila pode conter todos os nós de uma camada inteira.
    • Complexidade de espaço: exponencial em .
    • nós no conjunto explorado e nós na borda.
    • Dominada pelo pelo tamanho da borda. Então .

Note que é assustadoramente ruim! Se a profundidade é grande, então o custo de tempo e memória é impraticável.


  • Se e , então o número de nós é .
  • Se precisarmos de 1000 bytes para armazenar cada nó e gerarmos um milhão de nós por segundo, temos:
    • Tempo: 350 anos
    • Memória: 10 exabytes 10 000 000 000 000 000 000 bytes

Busca em Profundidade (DFS)

  • Sempre expande o nó mais profundo na borda atual da árvore de busca
  • Estrutura principal: pilha LIFO (ou recursão implícita).
  1. Inserir o nó inicial na pilha.
  2. Repetir enquanto a pilha não estiver vazia:
    a. Remover o topo n.
    b. Se n é objetivo, retornar caminho até n.
    c. Expandir n, gerando todos os sucessores e inserindo-os na pilha (apenas se ainda não foram visitados).

Busca em Profundidade (DFS)

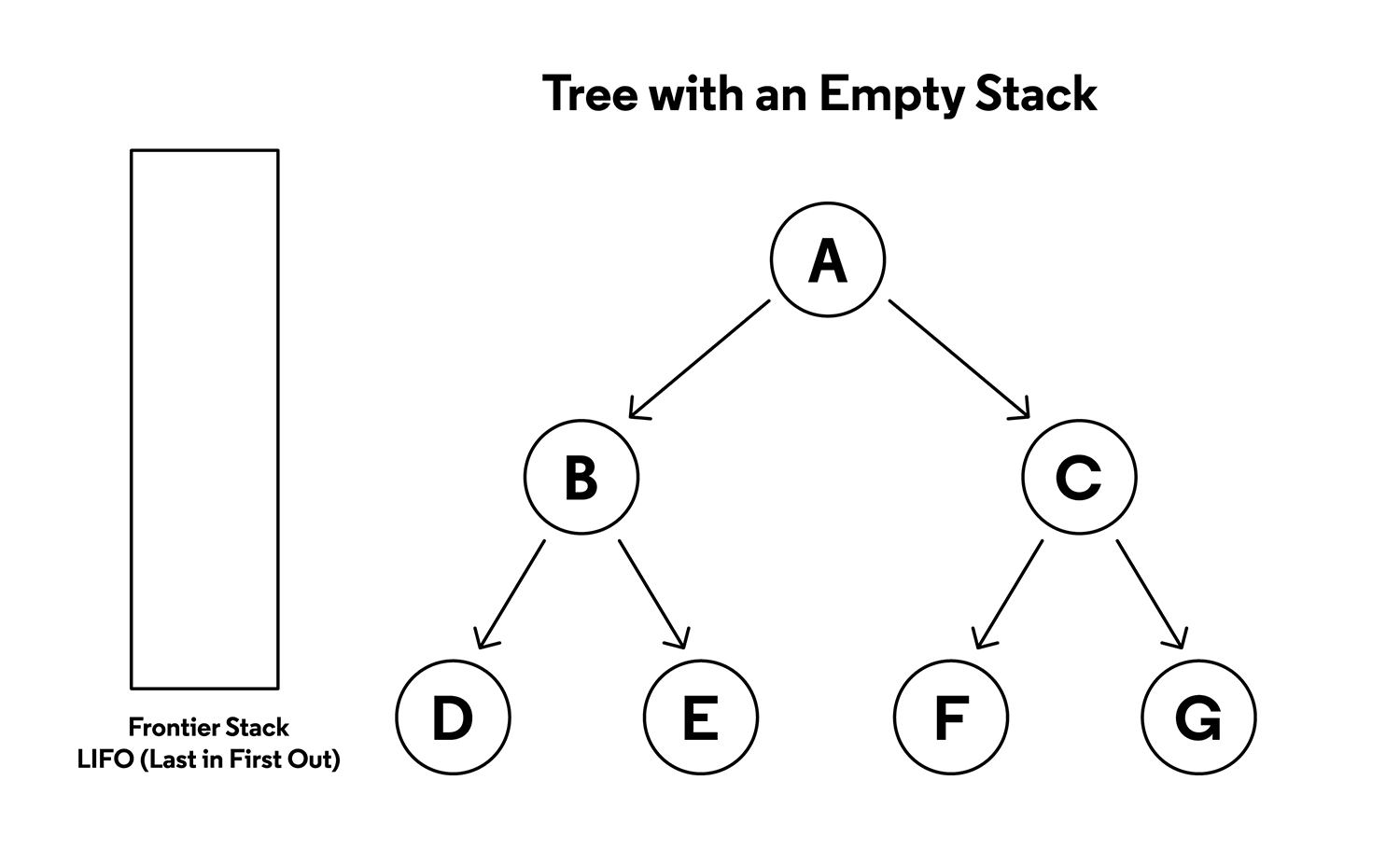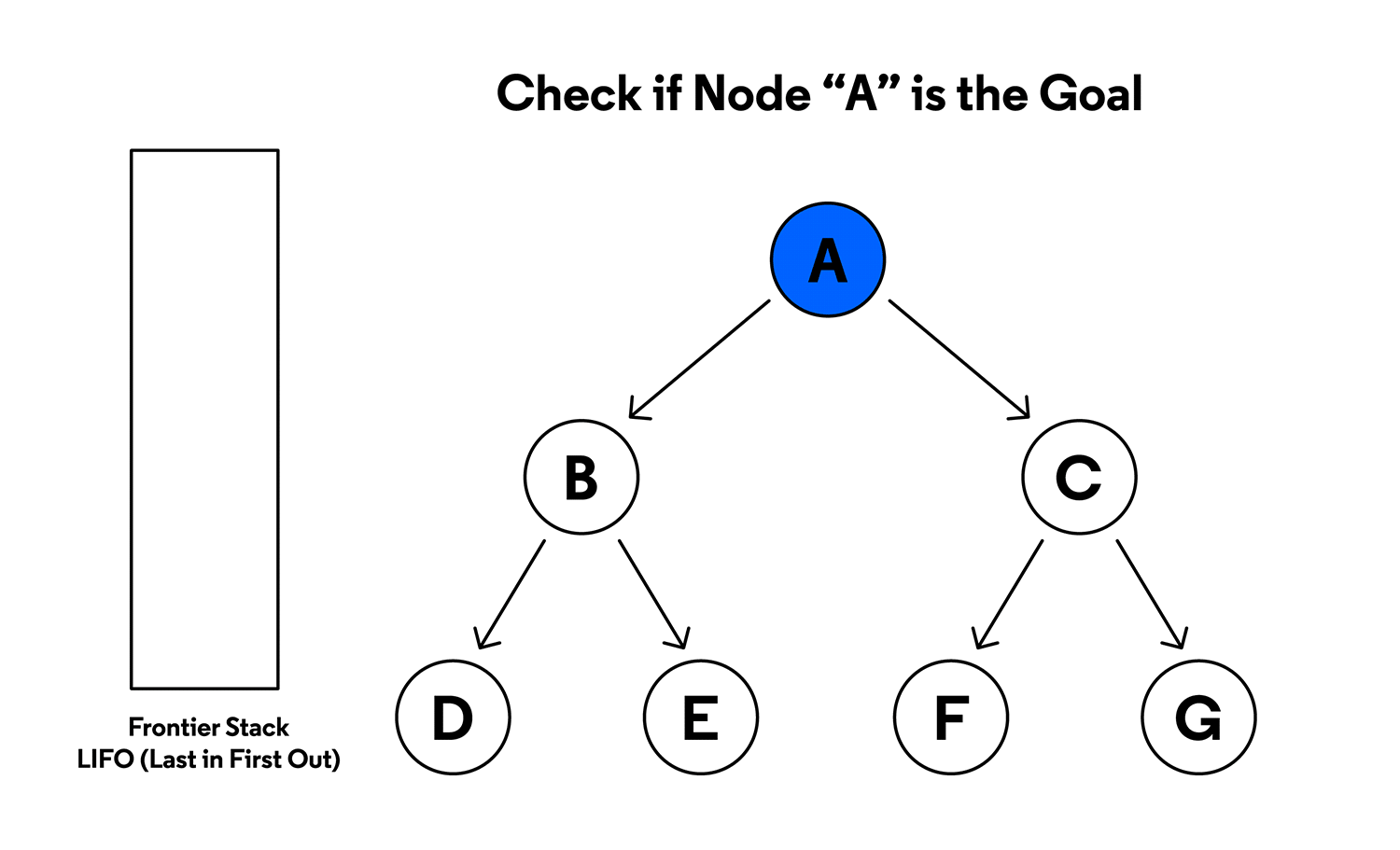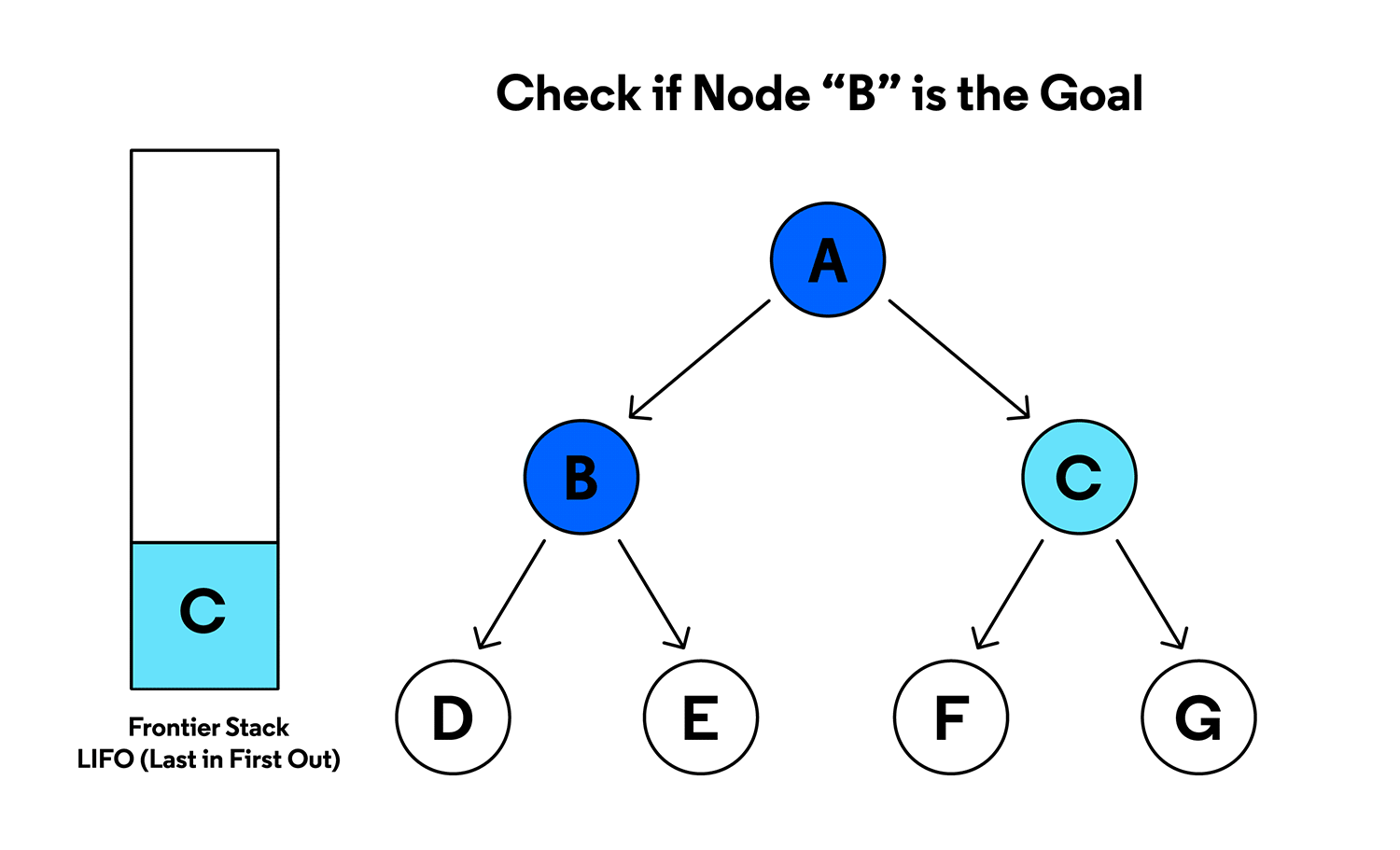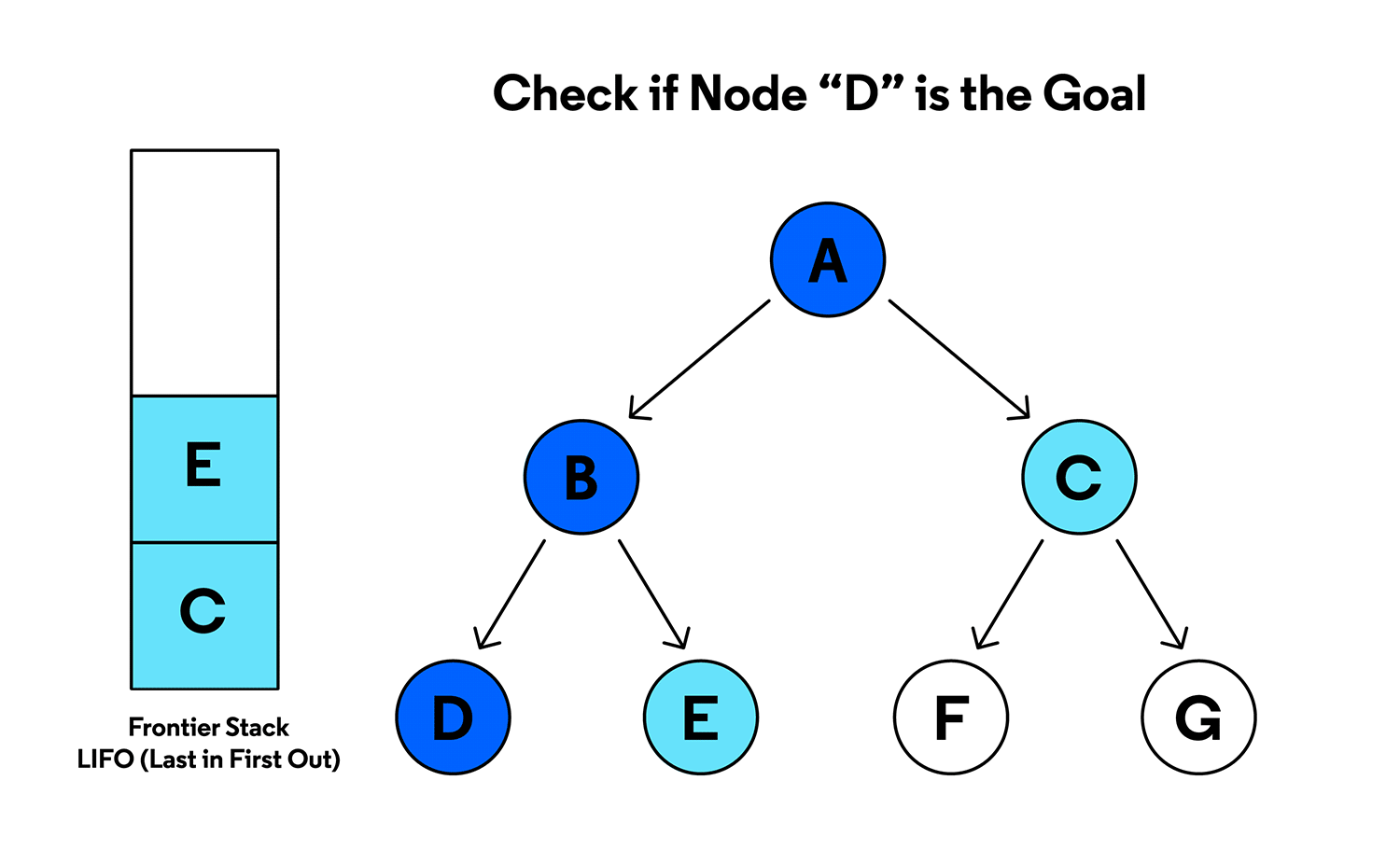
Fonte: https://www.codecademy.com/article/bfs-vs-dfs

DFS: Completude e Otimalidade

  • Completude: a versão da busca em grafos, que evita estados repetidos e
    caminhos redundantes, é completa em espaços de estados finitos porque acabará por expandir cada nó. A versão da busca em árvore não é completa.
  • Otimalidade: não garante caminho mínimo (mesmo que o grafo tenha custo uniforme); apenas encontra uma solução.

DFS: Complexidade

  • Complexidade de tempo: .
    • No pior caso expande todos os nós até a profundidade , onde é a profundidade máxima de qualquer nó e é o fator médio de sucessão.
    • Mas tende a operar melhor quando a solução está em nós-folha mais à esquerda.
  • Complexidade de espaço: .
    • Armazena apenas o caminho atual + nós pendentes na pilha.
    • Proporcional à profundidade máxima alcançada.
    • Uma vez que um nó é expandido, ele pode ser removido da memória, assim que todos os seus descendentes tenham sido explorados.
    • Nas métricas utilizadas anteriormente: 156 kilobytes, em vez de 10 exabytes na profundidade .

Observações

  • DFS é preferido quando o espaço de estados é vasto e a solução está mais profunda ou quando não se requer caminho mínimo.
  • BFS garante, em grafos de custo uniforme, que o primeiro nó encontrado na profundidade d corresponde ao caminho mais curto; porém essa garantia vem à custa de um maior uso de memória.

Busca em profundidade limitada

  • Objetivo: combinar a simplicidade da Busca em Profundidade com controle explícito sobre a profundidade máxima explorada, evitando explorações infinitas em grafos recursivos ou ilimitados.
  • Estrutura de dados principal: pilha LIFO (ou recursão) acompanhada de um parâmetro limite que indica a profundidade máxima permitida.
  • Busca Iterativa
  • Duas versões:
    • Limitada (Depth Limited Search - DLS): onde definimos um limite e não o alteramos
    • Iterativa (Iterative Depth Search): onde o limite vai sendo aumentado iterativamente

DLS: Busca em profundidade limitada

  1. Iniciar com o nó raiz na pilha, profundidade atual = 0.
  2. Enquanto a pilha não estiver vazia:
    • Remover o topo n.
    • Se n é solução → retornar caminho até n.
    • Se profundidade atual < limite: expandir n, inserir sucessores na pilha com profundidade +1 (apenas se ainda não visitados).
  3. Se a pilha esvaziar sem encontrar solução → falha de busca.

Busca em profundidade limitada: Complexidades

  • Tempo: – no pior caso expande todos os nós até a profundidade ( = fator médio de sucessão).
  • Espaço: – pilha armazena apenas o caminho atual e o limite máximo.

Busca em profundidade limitada: Completude e Otimalidade

  • Completude: Se a solução existe, ela será encontrada, desde que a profundidade da árvore seja finita e menor que a profundidade escolhida; sempre encontrará solução (existente) caso a profundidade seja iterativa.
  • Otimalidade: não assegurada; pode retornar uma solução que não seja de menor custo ou profundidade.

Busca em Profundidade Iterativa (IDDFS)

  • Objetivo: Combinar a completude de uma busca em largura com o consumo de memória mínimo de uma busca em profundidade, por meio da execução iterativa de buscas em profundidade limitada cujo limite aumenta gradualmente.
  • Princípio de funcionamento
    1. Para l = 0, 1, 2, … executar Busca em Profundidade Limitada (DLS) até a profundidade l.
    2. Se o nó‑objetivo for encontrado numa das iterações, retornar o caminho correspondente.
    3. Caso contrário, incrementar l e repetir.

IDDFS: Complexidades

  • Tempo: – cada nível de profundidade é revisitado apenas vezes (o fator médio de sucessão), resultando em custo assintótico equivalente a uma única busca em largura na profundidade ótima .
  • Espaço: – no pior caso, armazena apenas o caminho atual e a pilha da última iteração.

IDDFS: Propriedades

  • Completude: garantida (o limite eventualmente alcança qualquer profundidade finita).
  • Otimalidade: assegurada quando todos os passos têm custo uniforme; IDDFS devolve um caminho de menor profundidade.
  • Robustez em grafos com ciclos: o controle explícito de profundidade evita vácuo infinito, enquanto a re‑exploração de nós já visitados não afeta a completude.

Desafios e Extensões

  • Busca em ambientes dinâmicos
  • Controle de recursos limitados (memória/tempo).
  • Busca com múltiplos objetivos (trade‑offs entre custos).
  • Integração de aprendizado: heurísticas aprendidas via RL ou ML.

Resumo e Próximos Passos

  • Representação do problema: Estado inicial, operações que geram novos estados, teste de objetivo e função de custo (quando aplicável).
  • Busca não-informada explora o espaço de estados sem utilizar nenhuma informação adicional.
  • A escolha entre DFS e BFS depende do trade‑off entre complexidade temporal e memória.
  • Próxima aula: Estratégias de Busca Informada.

center

Atividade recomendada: Leitura do capítulo 3.

Perguntas para Discussão

  • Em termos simples, como a Busca em Profundidade (DFS) se comporta de maneira diferente da Busca em Largura (BFS) quando explorando o mesmo grafo?
  • Explique com suas próprias palavras o que significam os termos "completude" e "ótimo" quando falamos de algoritmos de busca.
  • Pense em um problema cotidiano (por exemplo, encontrar o caminho mais curto entre duas cidades usando um mapa). Qual algoritmo de busca você escolheria para resolver esse problema e por quê?

- A busca prossegue imediatamente até o nível mais profundo da árvore de busca, onde os nós não têm sucessores (folhas). - À medida que esses nós são expandidos, eles são retirados da borda e, então, a busca "retorna" ao nó seguinte mais profundo que ainda tem sucessores inexplorados.

# Estratégias de Busca Informada **Algoritmos baseados em avaliação**: $f(n) = g(n) + h(n)$. - $g(n)$: custo acumulado até o nó $n$. - $h(n)$: estimativa heurística do restante. *Tipos de heurísticas:* admissíveis, consistentes, e seu impacto na optimalidade. ---

# Algoritmos Populares - **Busca A\*** – Garante solução ótima se $h$ é admissível e consistente; usa prioridade pelo menor $f(n)$. - **Greedy Best‑First Search** – Usa apenas $h(n)$; rápido, mas sem garantias de optimalidade.

# Heurísticas: Exemplos e Construção - **Heurística admissível**: distância Euclidiana no problema do 8‑puzzle. - **Heurística consistente**: soma das distâncias de Manhattan; satisfaz a desigualdade triangular. ---