Como medir se estamos chegando no objetivo
no contexto do 8-puzzle?
Como medir se estamos chegando no objetivo
no contexto do 8-puzzle?
Heurística: Distância de Manhattan
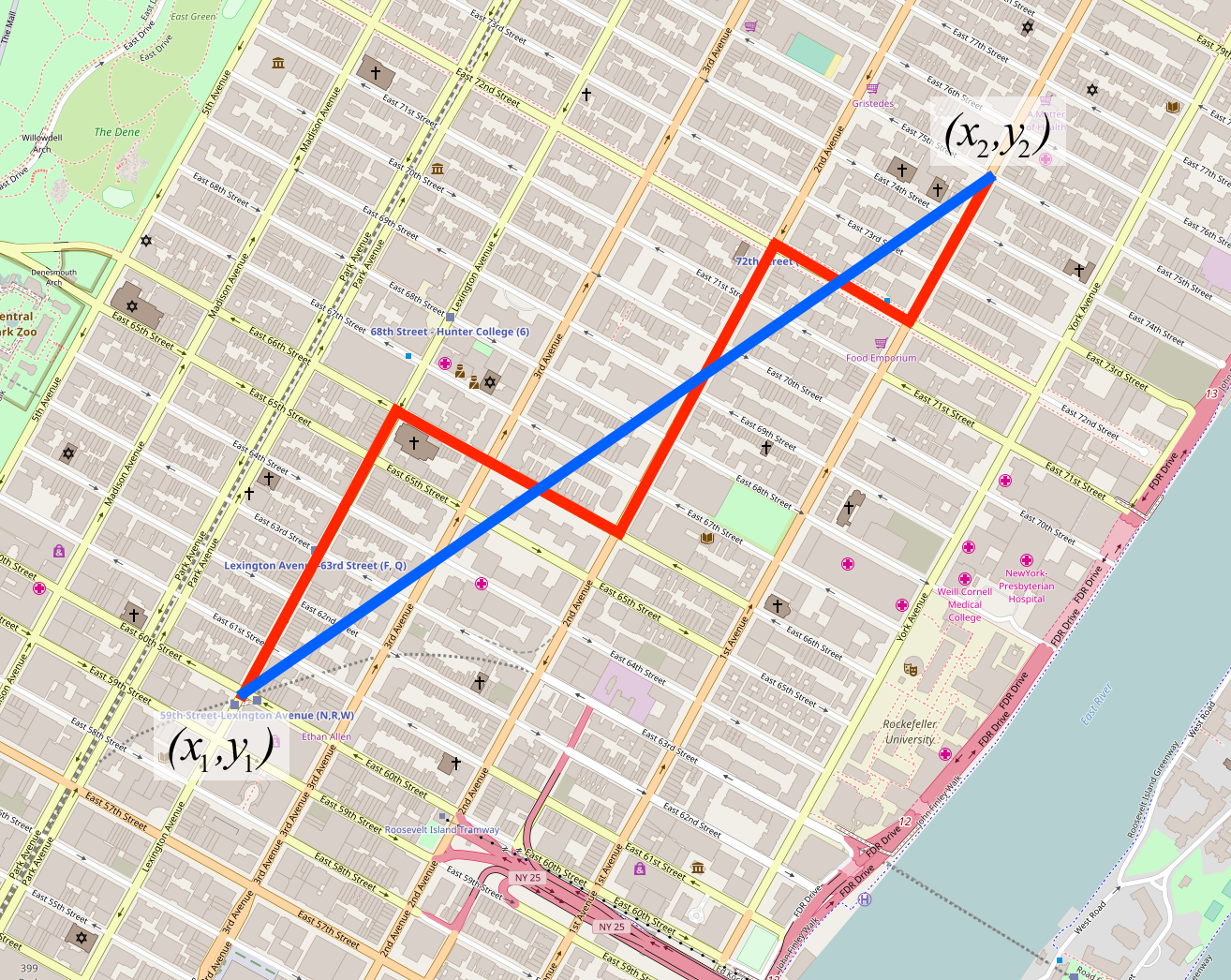
Distância de Manhattam (em vermelho) e distância Euclideana (em azul). Fonte: Machine Learning with Swift.
Distância de Manhattam (em azul) e distância Euclideana (em verde). Fonte: DataCamp.
Heurística: Distância de Manhattan
A distância de Manhattan mede o número total de movimentos horizontais e verticais necessários para levar cada peça de sua posição atual até a posição correta.
onde:
Estado inicial:
2 8 3
1 6 4
7 5
Objetivo:
1 2 3
8 4
7 6 5
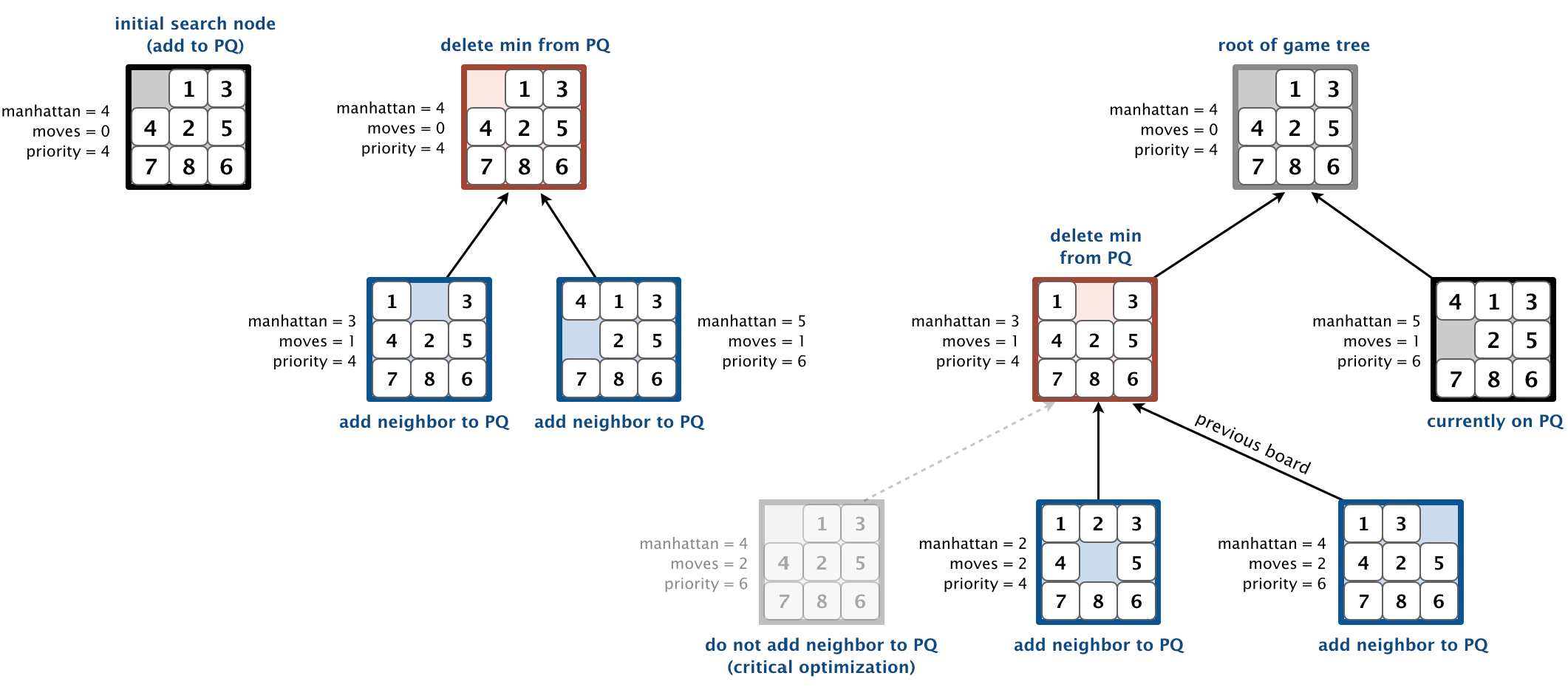
Fonte da imagem: https://8-puzzle.readthedocs.io/en/latest/
Heurística: Distância de Manhattan
- Admissível?
- Sim: nunca superestima o custo real.
- Fácil de implementar?
- Sim: simples e eficiente
Uma heurística é admissível se
nunca superestima o custo real até o objetivo.
A Distância de Manhattan é considerada uma heurística mais eficaz que apenas contar peças fora do lugar?
Definição Formal de Heurística
Seja
- Função heurística:
- Admissibilidade:
- Não superestima o custo real
- Heurísticas admissíveis são otimistas por natureza porque imaginam que o custo de resolver o problema seja menor que realmente é.
- Não superestima o custo real
Exemplo: Distância entre Cidades da Romênia
Considere encontrar o melhor caminho entre as cidades de Arad (estado inicial) e Bucharest (estado objetivo).

Qual heurística você usaria para encontrar um bom (ou o melhor) caminho entre
Arad e Bucharest?
Exemplo: Distância entre Cidades da Romênia (cont.)
A tabela à direita da imagem mostra distância em linha reta estimada de cada cidade presente no mapa até à capital do país, Bucharest.

Greedy Best‑First Search (Busca Gulosa)
A cada passo escolhe a ação que parece mais promissora no presente.
- Baseia‑se em uma função heurística
- Não considera custos acumulados, apenas a decisão local.
- Expande o nó com menor heurística. A decisão tomada nunca é revista.
- Estrutura de dados: Fila de prioridade (min-heap)
- Completeness: não garante solução se houver ciclos e heurística inválida.
- Optimality: não garantida (pode escolher caminhos sub‑óptimos).
- Aplicações em Tempo Real: Planejamento de rotas de robôs, jogos (IA de NPCs) onde respostas rápidas são importantes.
Greedy Best-First: Voltamos ao exemplo anterior. Vamos encontrar o caminho mais curto:
(A) de Arad a Bucharest. (B) de Iasi para Fagaras.

A* (A-estrela)
- Função:
- g(n): custo acumulado do caminho já percorrido até
- h(n): estimativa heurística do custo de
- g(n): custo acumulado do caminho já percorrido até
- Estrutura de dados: Fila de prioridade ordenada por
- Se
- Se custos forem positivos.
- Se o fator de ramificação
- Consistência (ou Monotonicidade):
- Observação – A consistência implica admissibilidade.
