Exemplo de Motivação (cont.)
- Variáveis:
- Domínio:
- Restrições:
- Solução:
- Uma solução possível
Fonte da Imagem: Resumos LEIC-A.
Busca com Satisfação de Restrições (CSP)
- CSP (Constraint Satisfaction Problem): Problema onde se busca uma atribuição de valores a variáveis que satisfaça todas as restrições.
- Componentes principais:
- Estado
- Domínio
- Restrições
- Unárias: sobre uma única variável
- Binárias: sobre duas variáveis
- N-árias: sobre várias variáveis
- Estado
- Solução: atribuição
N-Queens: Exemplo clássico de CSP
- Objetivo: Queremos colocar exatamente uma rainha em cada linha do tabuleiro, sem que nenhuma delas ataque outra.
- Coluna: duas rainhas não podem ficar na mesma coluna.
- Diagonal: duas rainhas não podem estar na mesma diagonal (tanto a diagonal que vai de canto superior esquerdo a inferior direito quanto a que vai de canto superior direito a inferior esquerdo).
- Complexidade: O número de soluções cresce super‑exponencialmente (para
- NP‑completo: possui
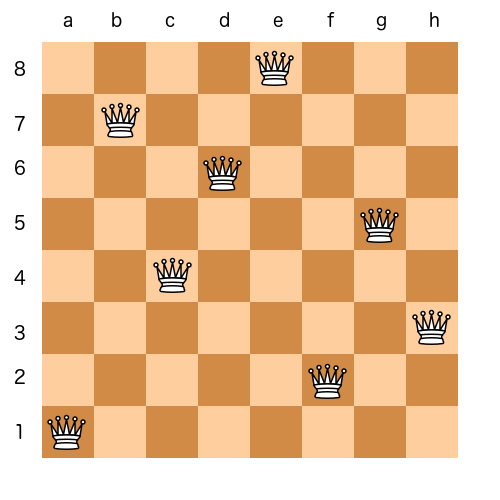
Fonte da Imagem: Paul Brown.
Vamos jogar o N-Queens Puzzle:
CSP no Cotidiano: Aplicações Práticas
| Área | Descrição |
|---|---|
| Planejamento de Rotas (GPS) | Variáveis = pontos de controle; restrições de tempo e distância. |
| Agendamento de Cursos | Horários, salas, professores → CSP com domínios discretos. |
| Design de Circuitos Digitais | Distribuição de componentes na placa → restrição de espaço. |
| Computação em Nuvem | Alocação de recursos, distribuição de dados |
| Data Marketplaces | Distribuição de ganhos em mercados de dados |
Sudoku: Mais um exemplo de CSP
- Tabuleiro
- Preencher todas as células com números
| Restrições |
|---|
| Cada linha contenha cada número exatamente uma vez. |
| Cada coluna contenha cada número exatamente uma vez. |
| Cada bloco contenga cada número exatamente uma vez. |
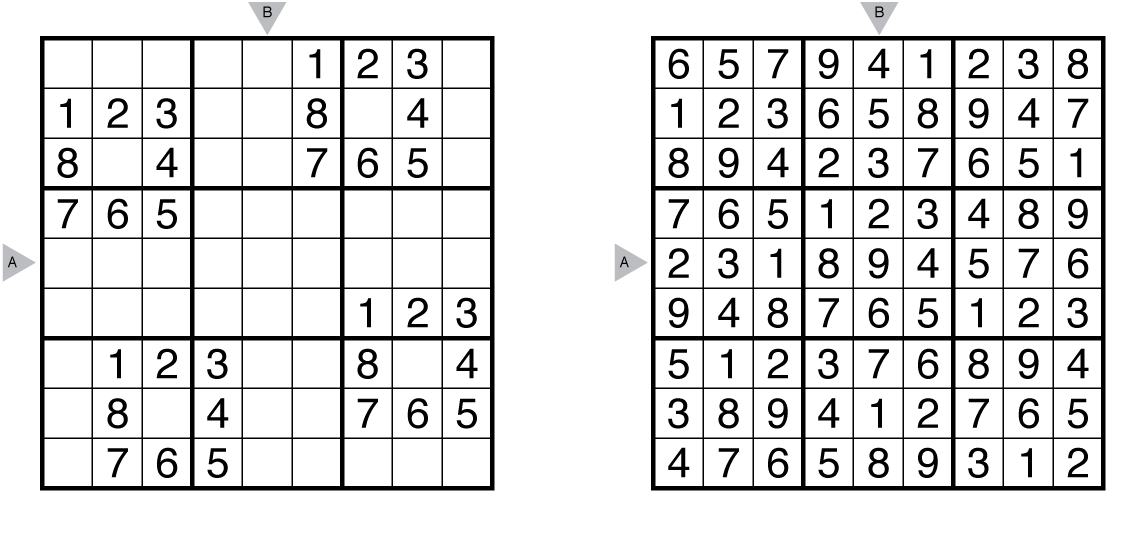
Fonte da Imagem: GM Puzzles.
Sudoku: Exemplo

Fonte da Imagem: Wikipedia.
Sudoku: Formalização
- Variáveis:
- Domínios:
- Restrições Binárias:
- Linha:
- Coluna:
- Bloco
- Linha:
- Restrições N‑Árias:
- Equivalentemente, cada conjunto (linha/coluna/bloco) deve conter valores distintos – pode ser expressa como restrição "todos diferentes".
- Problema de Busca:
Sukodu: Modelagem
- Domínio:
- Restrição de Linha:
- Restrição de Coluna:
- Restrição de Bloco: Para bloco
- Solução:
Algoritmo por Força Bruta
- Explora todas as combinações de valores.
- Útil apenas para problemas pequenos (ex.: Sudoku,
- Complexidade:
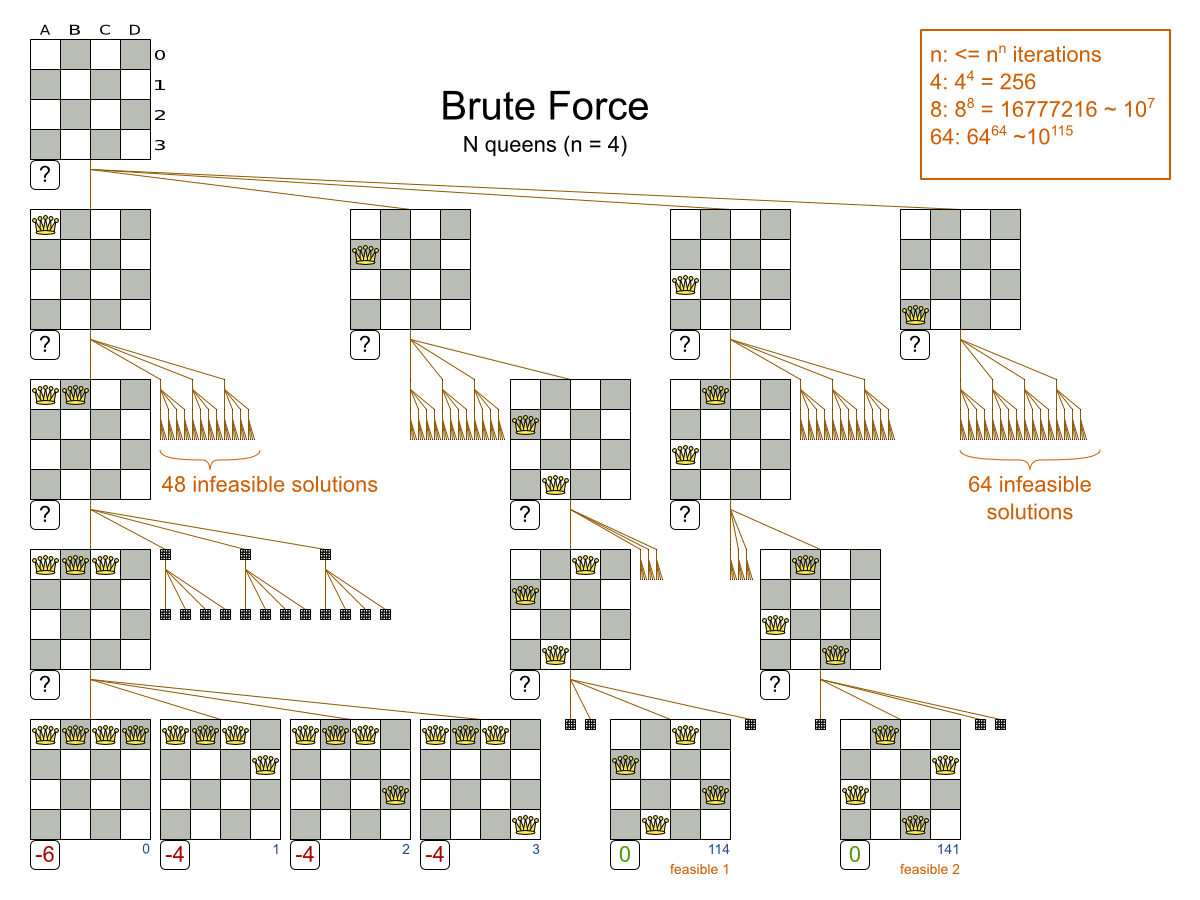
Backtracking
- DFS não considera informações sobre restrições: continua percorrendo o grafo de busca mesmo que uma restrição já tenha sido violada.
- Exploração inútil
- Pode ser aplicado a CSPs sem modificações, porém a taxa de sucesso depende fortemente da ordem de atribuição.
- Backtracking: Variante especializada do DFS que incorpora checagem de consistência no momento da atribuição.
- Ao detectar violação de restrição, revira imediatamente para o nível anterior (backtrack), evitando a exploração de sub‑árvores inviáveis.
- Integra heurísticas de escolha de variável e valor (MRV, LCV) que reduzem drasticamente o espaço de busca em CSPs típicos.
- Exige manutenção adicional de estruturas de dados (domínios restritos, histórico de escolhas), aumentando a sobrecarga de memória.
Backtracking N-Queens
![]()
Fonte da Imagem: ResearchGate.
- Coloque cada rainha, uma por uma, em linhas diferentes.
- Ao colocar uma rainha em uma linha, verifique se há conflitos com as rainhas já colocadas.
- Para qualquer coluna, se não houver conflito, marque essa linha e coluna como parte da solução, colocando a rainha.
- Caso não seja encontrada nenhuma célula segura devido a conflitos, volte atrás (ou seja, desfaça a colocação da rainha mais recente).
Backtracking: Sudoku
- Procedimento recursivo: escolhe uma variável, tenta um valor do domínio e verifica restrições locais.
- Se falhar, volta ("backtrack") ao passo anterior.
function BACKTRACK_SUDOKU(board):
if board is complete: return board
(r,c) = select_unassigned_cell(board) // MRV + LCV
for val in order_domain_values(r,c,board): // LCV
if consistent(r,c,val,board):
board[r][c] = val
result = BACKTRACK_SUDOKU(board)
if result != failure: return result
board[r][c] = 0 // undo
return failure
Backtracking: Colorir Mapa
Fonte da Imagem: Resumos LEIC-A.
Forward Checking (FC)
- Após atribuir
- Se algum domínio ficar vazio → falha imediata.
Complexidade amortizada:
Heurísticas de Seleção
| Estratégia | Descrição |
|---|---|
| MRV (Minimum Remaining Values) | Escolhe variável com menor domínio restante. |
| Degree | Entre MRV‑iguais, escolhe a que tem mais restrições não resolvidas. |
| LCV (Least Constraining Value) | Ordena valores que restringem menos os vizinhos. |
Restrições Leves (Soft Constraints)
- Também é possível definir restrições que podem ser quebradas
- Geralmente associadas a um custo ou preferências
- Ex.: Priorizar o uso das cores na ordem vermelho, verde, azul
- Pode ser resolvido associando custos à cada valor do domínio, podendo ser tratado como problema de otimização
- Também pode ser resolvido ordenando a expansão da busca
Resumo e Próximos Passos
- CSP (Constraint Satisfaction Problem): Variáveis, domínios e restrições definem o problema. Objetivo é encontrar uma atribuição que satisfaça todas as restrições.
- Backtracking (exaustivo + heurísticas).
- Forward Checking – eliminação antecipada de valores impossíveis.
- Heurísticas de escolha: MRV (Minimum Remaining Values) e LCV (Least Constraining Value).
- Aplicações clássicas: Sudoku, Xadrez, otimização logística, etc.
- Próximos passos:
- Implementar força bruta e backtracking.
- Algoritmos evolutivos e meta‑heurísticas.

Atividade recomendada: Leitura do capítulo 3.
Perguntas e Discussão
- Qual a diferença fundamental entre backtracking puro e forward checking? Em que situações o custo adicional do forward checking vale a pena?
- Como a heurística MRV (Minimum Remaining Values) influencia a profundidade da árvore de busca? Pode haver casos em que escolher a variável com mais valores restantes seja mais vantajoso?
- Como a escolha do modelo de domínio (por exemplo, representar cada linha como uma variável vs. usar variáveis binárias para cada célula) afeta a eficiência das técnicas de CSP? Quais trade‑offs surgem na modelagem de problemas com muitos valores distintos por variável?
- Quais são os principais desafios ao adaptar algoritmos de CSP para domínios contínuos ou híbridos (contínuo + discreto)?