Exemplo de Vizinhança
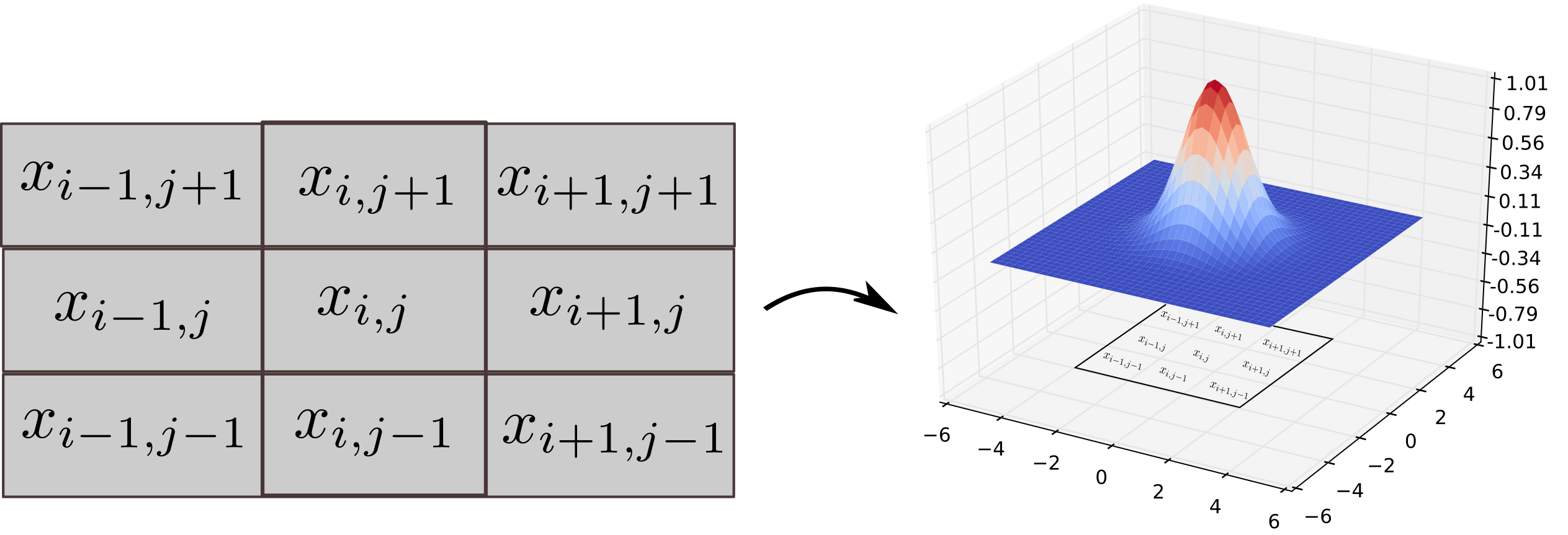
Exemplo de coordenadas para vizinhança em Hill Climbing. Fonte: Andres Mendez-Vazquez
A versão mais comum é o Hill Climbing Simples (ou First-Choice Hill Climbing), que seleciona o primeiro vizinho que oferece melhoria.
função HILL_CLIMBING(h, s0):
s ← s0
Para v em N(s):
Se h(v) > h(s) então:
s ← v
retorna s

Exemplo de coordenadas para vizinhança em Hill Climbing. Fonte: Andres Mendez-Vazquez
state[i]=j. Um vetor de i, linha j.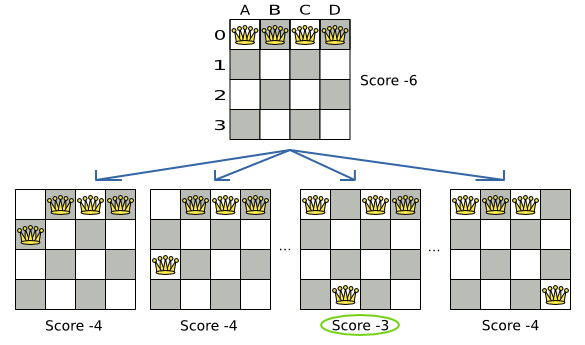
N-Rainhas com Hill Climbing. Fonte: Optaplanner.

Exemplo de Gradiente Descendente. Fonte: Digital Ocean.
A principal fraqueza do Hill Climbing é sua natureza gulosa, que o impede de explorar o espaço de busca de forma global, resultando na paralisação.
| Limitação | Descrição |
|---|---|
| Máximo Local (Local Maximum) | O algoritmo fica preso em um pico que é inferior ao máximo global, pois todos os movimentos vizinhos resultam em piora. |
| Platô (Plateau) | Região plana onde todos os vizinhos têm o mesmo valor objetivo. O algoritmo não consegue decidir qual direção seguir e pode ser incapaz de achar a saída (exceto em casos de shoulders). |
| Cordilheira (Ridge) | Uma sequência de máximos locais que forma uma crista ascendente. Exige movimentos combinados que o Hill Climbing pode não ser capaz de realizar em um único passo, levando-o a parar. |
As variações buscam introduzir mecanismos de Exploração para escapar dos máximos locais, equilibrando-a com a Exploitação inerente ao Hill Climbing.
| Limitação | Explicação |
|---|---|
| Padrões locais | Pode ficar preso em ótimos que não são globais. |
| Sensibilidade à inicialização | Resultado depende da solução inicial |
| Vizinhança limitada | Se a vizinhança for pequena, melhorias podem ser insuficientes. |
| Convergência lenta | Em espaços de alta dimensionalidade pode exigir muitas iterações. |
* Ao contrário dos algoritmos de busca tradicionais (que exploram sistematicamente e mantêm caminhos na memória), a Busca Local opera usando **apenas um único estado atual**.
* **Analogia:** O algoritmo de Hill-Climbing guarda uma **forte semelhança** com o Gradient Ascent, mas depende de uma operação estocástica (`Tweak`) para explorar vizinhos, e não do cálculo do gradiente.
* **Vantagem:** Maior garantia de seguir o melhor caminho local possível (maior **Exploitação**). * **Desvantagem:** Alto custo computacional, pois exige a avaliação de todos os vizinhos gerados (amostras) antes de cada movimento.
* **Vantagem:** Reduz o custo de computação (em comparação ao Steepest Ascent) e introduz um elemento de **Exploração**. * **Versão First Choice:** O algoritmo mais simples: seleciona o **primeiro vizinho** que melhora o estado atual.
* **Estratégia:** Se uma instância cair em um máximo local, o processo é abortado, e a busca é reiniciada em outro ponto do espaço de busca. * **Classificação:** É um **algoritmo de otimização global**. Se executado por tempo suficiente, está garantido a encontrar o ótimo global, pois eventualmente um reinício cairá na "encosta" certa.