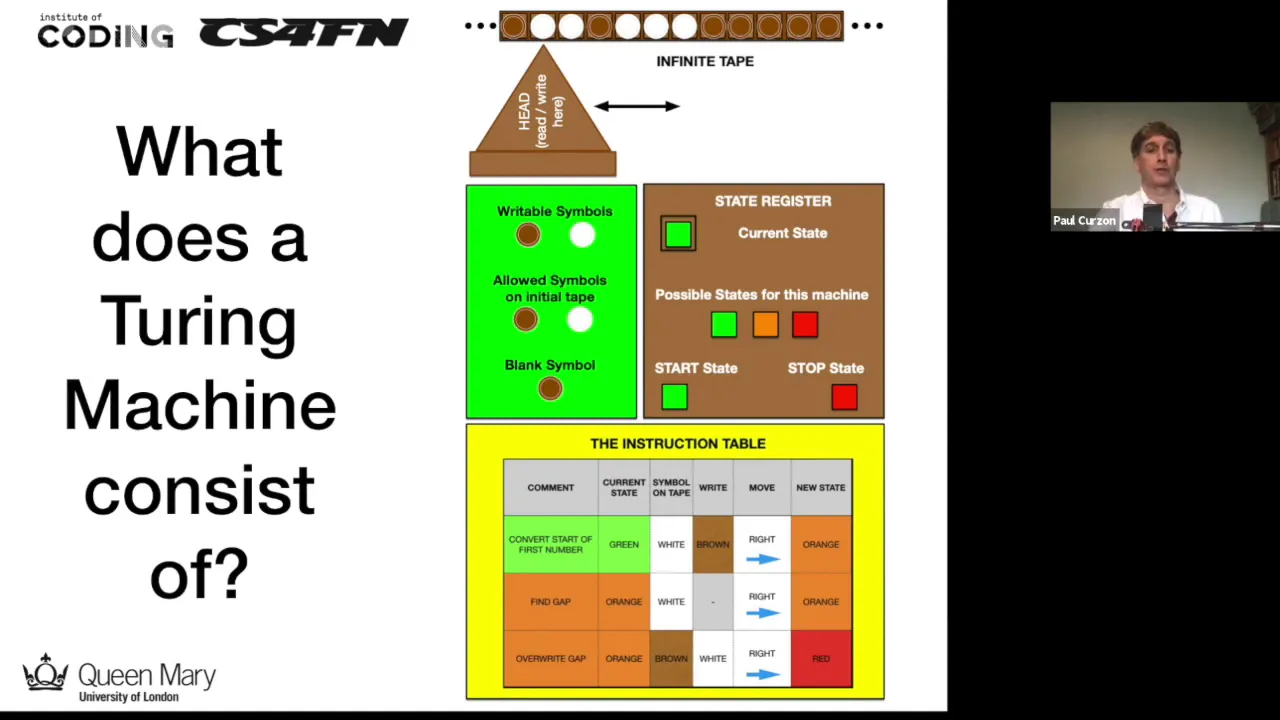
Modelo Físico de uma MT.
Note que a natureza nos impede de ter uma fita infinita. Veja mais em: https://aturingmachine.com
Definição de Máquina de Turing
- Definição (Máquina de Turing): uma MT é uma 7-upla
Funcionamento de uma Máquina de Turing
- O Funcionamento geral de uma MT
- A cadeia
- A MT começa com o cursor na posição mais à esquerda
- A computação procede de acordo com a função de transição
- Quando em um estado
- Escreve 'b' na fita no lugar de 'a'; e
- Move o cursor para a esquerda ou para direita.
- Quando em um estado
- A computação continua até que
- A cadeia
- Pergunta: O que acontece se o cursor estiver mais à esquerda e a transição tenta mover o cursor à esquerda com
- Resposta: Nenhum movimento é feito.
Exemplo
Funcionamento de uma MT que reconhece
O diagrama de estados e transições está ilustrado ao lado.
Vamos verificar a cadeia de exemplo
Exercício: Descreva o diagrama de estados de uma MT que reconhece
Configuração de uma Máquina de Turing
Descrição instantânea
- Uma configuração de uma MT descreve:
- Seu estado atual;
- O conteúdo da fita; e
- A posição atual do cursor de leitura/escrita.
- Representação:
- Dizemos que uma configuração
- Exemplos:
Definição de aceite
Dizemos que uma MT
onde:
- (1)
- (2) Cada
- (3)
A MT rejeita
Variantes de uma MT
- Expandem o modelo padrão para explorar diferentes aspectos de computação.
- MT Multifitas: possuem várias fitas para leitura e escrita simultânea, aumentando a eficiência.
- MT Não-Determinísticas: permitem múltiplos caminhos de execução ao mesmo tempo.
- Essas variações ajudam a entender questões como eficiência, paralelismo e universalidade no processamento computacional.
- Robustez: Reconhecem a mesma classe de linguagens. Ou seja, possuem o mesmo poder computacional.
MT Multifitas
- Utiliza várias fitas, cada uma com seu próprio cursor de leitura/escrita.
- Isso permite que a máquina leia e escreva em múltiplas posições simultaneamente, tornando-a mais eficiente em certos problemas.
- A função de transição é ajustada para lidar com o estado atual e os símbolos lidos em todas as fitas, determinando o próximo estado, os símbolos a serem escritos e os movimentos das cabeças de leitura/escrita em cada fita.
- Equivalência ao modelo padrão: qualquer multifita pode ser simulada por uma MT de fita única.
- Ideia de prova: Concatenar as k fitas na fita S com o delimitador
Pergunta
- A definição que vimos é de uma MT determinística. Qual modificação precisa ser feita para torná-la Não-Determinística?
- Alterar
- Alterar
- Alterar
- Alterar
- Resposta: B
MT Não-Determinística
- Modificamos a função de transição:
- Assim como nos Autômatos Finitos, o não-determinismo não acrescenta poder computacional às MTs.
MT Não-Determinística
- Equivalência: Uma MT Não-Determinística é equivalente a uma MT padrão
- Uma MT Não-Determinística aceita uma cadeia se pelo menos um ramo leva ao estado de aceitação.
- Ideia de Prova: Simular uma MT Não-Determinística com uma MT de 3 fitas. Busca em largura na árvore de computação.
Linguagem Reconhecida por uma Máquina de Turing
- Todas as cadeias aceitas por uma MT
- Note que
- Rejeitar
- Nunca parar: entrar em loop infinito
- Rejeitar
- O conjunto de linguagens que podemos aceitar usando uma MT é chamado linguagens recursivamente enumeráveis.
- Linguagens recursivas são aquelas que podem ser decididas por uma MT que sempre para.
Tese de Church-Turing
- A Tese Church-Turing propõe que qualquer cálculo ou problema que possa ser resolvido por um algoritmo pode ser realizado por uma Máquina de Turing.
- Embora não seja formalmente provada, é amplamente aceita como a definição prática de computabilidade.
Dica Cultural
- Filme: O Jogo da Imitação (2014)
- Atualmente, 8/10 no IMDb
- Um pouco da história de Turing
- Doodle de 23 Junho de 2012 (Google)
- https://doodles.google/doodle/alan-turings-100th-birthday/
- Código aberto (Javascript)
Mais uma Dica

YouTube: https://www.youtube.com/watch?v=YzXoFldEux4.
Baseado no artigo https://arxiv.org/pdf/1904.09828.
Código Python: https://github.com/Cerno-b/mtg-turing-machine
Mais outra Dica
YouTube: https://youtu.be/soJ3FPvs7QI?si=rLK59BfBtNpnLUVZ.
Leia mais em https://teachinglondoncomputing.org/turingmachine/