Modelo GPT - Parte 1

Tópicos em Ciência de Dados

Prof. Dr. Denis Mayr Lima Martins

Pontifícia Universidade Católica de Campinas

Objetivos de Aprendizagem

• Implementar um modelo de LLM semelhante ao GPT que pode ser treinado para gerar texto.
• Compreender o conceito de normalização de camadas e sua importância no treinamento de redes neurais.
• Entender como conexões de atalho (skipping connections) em redes neurais profundas ajudam no treinamento.
• Implementar blocos Transformer para criar modelos GPT de diferentes tamanhos

Baseado no Livro Build a Large Language Model From Scratch de Sebastian Raschka Code repository: https://github.com/rasbt/LLMs-from-scratch

import os
os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"

• import os: Importa o módulo os para interagir com o sistema operacional.
• os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE": Define uma variável de ambiente que instrui a biblioteca MKL da Intel a permitir que múltiplas instâncias da mesma biblioteca sejam carregadas simultaneamente, sem gerar erro. Tal configuração costuma ser empregada para resolver conflitos entre bibliotecas em tarefas de computação científica ou aprendizado de máquina.

from importlib.metadata import version

import matplotlib
import tiktoken
import torch

print("matplotlib version:", version("matplotlib"))
print("torch version:", version("torch"))
print("tiktoken version:", version("tiktoken"))

matplotlib version: 3.10.5
torch version: 2.8.0
tiktoken version: 0.11.0

1. Codificando uma Arquitetura de LLM

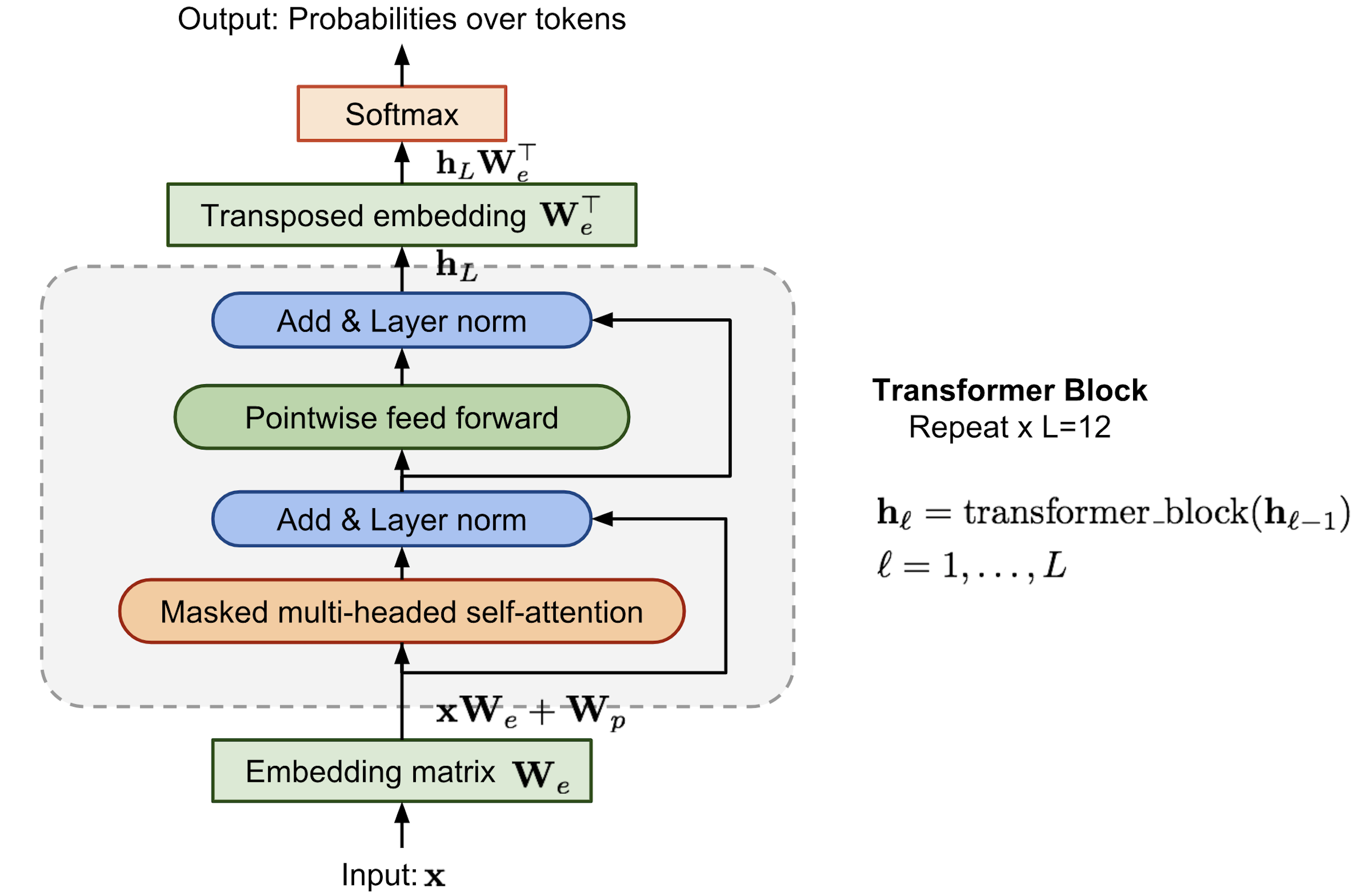
• Modelos de linguagem de larga escala (LLMs), como o GPT, são arquiteturas de redes neurais profundas projetadas para gerar novo texto palavra (ou token) por palavra. Apesar do tamanho, a arquitetura do modelo é menos complicada do que se imagina, já que muitos de seus componentes são repetidos.
• A arquitetura de um GPT contém, ao lado das camadas de embedding, blocos transformer que incluem o módulo de atenção multi-cabeças mascarada implementado anteriormente.

GPT_CONFIG_124M = {
    "vocab_size": 50257,    # Vocabulary size
    "context_length": 1024, # Context length
    "emb_dim": 768,         # Embedding dimension
    "n_heads": 12,          # Number of attention heads
    "n_layers": 12,         # Number of layers/transformer blocks
    "drop_rate": 0.1,       # Dropout rate
    "qkv_bias": False       # Query-Key-Value bias
}

• "vocab_size" tamanho de vocabulário de 50257 palavras, suportado pelo tokenizador BPE.
• "context_length" contagem máxima de tokens de entrada do modelo, conforme habilitado pelos embeddings posicionais.
• "emb_dim" tamanho do embedding para os tokens de entrada, convertendo cada token de entrada num vetor de 768 dimensões.
• "n_heads" número de cabeças de atenção no mecanismo de multi‑head attention.
• "n_layers" número de blocos transformer dentro do modelo, que iremos implementar em breve.
• "drop_rate" descarta 10% das unidades ocultas durante o treinamento para mitigar overfitting.
• "qkv_bias" decide se as camadas Linear no mecanismo de MHA devem incluir um vetor de bias ao calcular os tensores query (Q), key (K) e value (V); desativaremos essa opção, prática padrão em LLMs modernos.

Implementação Principal

Arquitetura inicial chamada que serve como esqueleto do modelo.

import torch
import torch.nn as nn

class SimpleGPTModel(nn.Module):
    def __init__(self, cfg):
        super().__init__()
        self.tok_emb = nn.Embedding(cfg["vocab_size"], cfg["emb_dim"])
        self.pos_emb = nn.Embedding(
            cfg["context_length"], cfg["emb_dim"])
        self.drop_emb = nn.Dropout(cfg["drop_rate"])
        self.trf_blocks = nn.Sequential(
            *[SimpleTransformerBlock(cfg) for _ in range(cfg["n_layers"])])
        self.final_norm = SimpleLayerNorm(cfg["emb_dim"])
        self.out_head = nn.Linear(
            cfg["emb_dim"], cfg["vocab_size"], bias=False)
    
    def forward(self, in_idx):
        batch_size, seq_len = in_idx.shape
        tok_embeds = self.tok_emb(in_idx)
        pos_embeds = self.pos_emb(
            torch.arange(seq_len, device=in_idx.device))
        x = tok_embeds + pos_embeds
        x = self.drop_emb(x)
        x = self.trf_blocks(x)
        x = self.final_norm(x)
        logits = self.out_head(x)
        return logits

Camadas adicionais

class SimpleTransformerBlock(nn.Module):
    def __init__(self, cfg):
        super().__init__()
        # Um placeholder simples

    def forward(self, x):
        # Este bloco não faz nada e apenas retorna sua entrada.
        return x

class SimpleLayerNorm(nn.Module):
    def __init__(self, normalized_shape, eps=1e-5):
        super().__init__()
        # Os parâmetros aqui são apenas para imitar 
        # a interface do LayerNorm.

    def forward(self, x):
        # Esta camada não faz nada e apenas retorna sua entrada.
        return x

Visão Geral

Visão Geral da Arquitetura GPT. Fonte: Ahead of AI.

Tokenização

A saída do código abaixo é o que a LLM recebe, e a tarefa consiste em produzir a próxima palavra desse texto.

import tiktoken

tokenizer = tiktoken.get_encoding("gpt2")

batch = []

txt1 = "Every effort moves you"  # every word will result in a token
txt2 = "Every day holds a"

batch.append(torch.tensor(tokenizer.encode(txt1)))
batch.append(torch.tensor(tokenizer.encode(txt2)))
batch = torch.stack(batch, dim=0)
print(batch)

tensor([[6109, 3626, 6100,  345],
        [6109, 1110, 6622,  257]])

Instanciando o Modelo

Inicializamos uma nova instância do SimpleGPTModel com 124 milhões de parâmetros conforme especificado acima e alimentamos o modelo com o lote tokenizado (os resultados do modelo são comumente denominados logits).

torch.manual_seed(123)
model = SimpleGPTModel(GPT_CONFIG_124M)  
logits = model(batch)                   
print("Output shape:", logits.shape)
print(logits)

Output shape: torch.Size([2, 4, 50257])
tensor([[[-1.2034,  0.3201, -0.7130,  ..., -1.5548, -0.2390, -0.4667],
         [-0.1192,  0.4539, -0.4432,  ...,  0.2392,  1.3469,  1.2430],
         [ 0.5307,  1.6720, -0.4695,  ...,  1.1966,  0.0111,  0.5835],
         [ 0.0139,  1.6754, -0.3388,  ...,  1.1586, -0.0435, -1.0400]],

        [[-1.0908,  0.1798, -0.9484,  ..., -1.6047,  0.2439, -0.4530],
         [-0.7860,  0.5581, -0.0610,  ...,  0.4835, -0.0077,  1.6621],
         [ 0.3567,  1.2698, -0.6398,  ..., -0.0162, -0.1296,  0.3717],
         [-0.2407, -0.7349, -0.5102,  ...,  2.0057, -0.3694,  0.1814]]],
       grad_fn=<UnsafeViewBackward0>)

O tensor de saída possui duas linhas correspondentes às duas amostras de texto. Cada amostra consiste em 4 tokens (um para cada palavra); cada token é um vetor de 50257 dimensões, o que corresponde ao tamanho do vocabulário do tokenizador.

Embeddings tem 50257 dimensões porque cada uma dessas dimensões representa um token único no vocabulário. Ao final deste episódio, quando implementarmos o código de pós‑processamento, converteremos esses vetores de 50257 dimensões de volta em IDs de token, que então poderemos decodificar em palavras.

2. Layer Normalization

Usamos a normalização de camada para melhorar a estabilidade e eficiência do treinamento de redes neurais.

• Ideia central: ajustar as ativações (saídas) de uma camada de rede neural de modo que tenham média zero e variância unitária, também conhecida como unit variance.
• Vantagem: Acelera a convergência para pesos efetivos e garante um treinamento consistente e confiável.
• Nas arquiteturas GPT‑2 e nos transformers, a normalização de camada costuma ser aplicada antes e depois do módulo de atenção multi‑cabeça e antes da camada de saída final.

Layer Normalization. Fonte: Ahead of AI.

Vamos observar como funciona a normalização de camada passando uma pequena amostra de entrada por uma camada neural simples; especificamente, recriamos o exemplo ilustrado na figura acima através do código seguinte, no qual implementamos uma camada neural com 5 entradas e 6 saídas que aplicaremos a dois exemplos de entrada.

torch.manual_seed(123)

# Cria 2 exemplos de treino com 5 features cada
batch_example = torch.randn(2, 5) 
batch_example

tensor([[-0.1115,  0.1204, -0.3696, -0.2404, -1.1969],
        [ 0.2093, -0.9724, -0.7550,  0.3239, -0.1085]])

layer = nn.Sequential(nn.Linear(5, 6), nn.ReLU())
out = layer(batch_example)
print(out)

tensor([[0.2260, 0.3470, 0.0000, 0.2216, 0.0000, 0.0000],
        [0.2133, 0.2394, 0.0000, 0.5198, 0.3297, 0.0000]],
       grad_fn=<ReluBackward0>)

# -1 torna invariante contra dimensões adicionais
mean = out.mean(dim=-1, keepdim=True) 
var = out.var(dim=-1, keepdim=True)

print("Mean:\n", mean)
print("Variance:\n", var)

Mean:
 tensor([[0.1324],
        [0.2170]], grad_fn=<MeanBackward1>)
Variance:
 tensor([[0.0231],
        [0.0398]], grad_fn=<VarBackward0>)

Ilustrando o cálculo

dim=-1 em Layer Normalization. Fonte: Ahead of AI.

# Aplica a normalização de camada aos resultados da camada anterior
# Consiste em subtrair a média e dividir pelo desvio padrão.
out_norm = (out - mean) / torch.sqrt(var)
print("Normalized layer outputs:\n", out_norm)

mean = out_norm.mean(dim=-1, keepdim=True)
var = out_norm.var(dim=-1, keepdim=True)

# melhora a visualização
torch.set_printoptions(sci_mode=False)
print("Mean:\n", mean)
print("Variance:\n", var)

Normalized layer outputs:
 tensor([[ 0.6159,  1.4126, -0.8719,  0.5872, -0.8719, -0.8719],
        [-0.0189,  0.1121, -1.0876,  1.5173,  0.5647, -1.0876]],
       grad_fn=<DivBackward0>)
Mean:
 tensor([[    -0.0000],
        [     0.0000]], grad_fn=<MeanBackward1>)
Variance:
 tensor([[1.0000],
        [1.0000]], grad_fn=<VarBackward0>)

Layer Norm (módulo)

class LayerNorm(nn.Module):
    def __init__(self, emb_dim):  # valores na dimensão do embedding
        super().__init__()
        self.eps = 1e-5
        # isso torna os valores treináveis
        self.scale = nn.Parameter(torch.ones(emb_dim))  
        self.shift = nn.Parameter(torch.zeros(emb_dim))

    def forward(self, x):
        mean = x.mean(dim=-1, keepdim=True)
        var = x.var(dim=-1, keepdim=True, unbiased=False)
        norm_x = (x - mean) / torch.sqrt(var + self.eps)  # eps evita divisão por zero
        return self.scale * norm_x + self.shift

        # shift não tem efeito aqui pois adiciona apenas zero; 
        # será relevante mais tarde durante o treinamento,
        # permitindo que a rede desfaça essa normalização; 
        # similarmente para scale

Layer Norm (aplicação)

ln = LayerNorm(emb_dim=5)
out_ln = ln(batch_example)
out_ln

tensor([[ 0.5528,  1.0693, -0.0223,  0.2656, -1.8654],
        [ 0.9087, -1.3767, -0.9564,  1.1304,  0.2940]], grad_fn=<AddBackward0>)

Modelo GPT - Parte 2

Tópicos em Ciência de Dados

Prof. Dr. Denis Mayr Lima Martins

Pontifícia Universidade Católica de Campinas

Baseado no Livro Build a Large Language Model From Scratch de Sebastian Raschka Code repository: https://github.com/rasbt/LLMs-from-scratch

Recapitulando a aula passada

Arquitetura Transformer. Fonte: https://lilianweng.github.io.

Post-LN versus Pre-LN. Fonte: Ahead of AI.

Aspectos Gerais de Arquitetura de LLMs

Pythia: A Suite for Analyzing Large Language Models Across Training and Scaling (2023). Fonte: Ahead of AI.

Feed-Forward com Ativação GELU

---

Vamos implementar uma camada composta de uma pequena rede neural que será usada como parte do bloco Transfomer nos LLMs.

Iniciaremos com a função de ativação.

Por que precisamos de funções de ativação não-lineares em Redes Neurais?

Importância das funções de ativação não-lineares. Fonte: Anjali Kumari.

Feed-Forward com Ativação GELU

• A função de ativação é a transformação não linear que fazemos ao longo do sinal de entrada.
• Quando não temos a função de ativação, os pesos e bias simplesmente fazem uma transformação linear. Uma equação linear é simples de resolver, mas é limitada na sua capacidade de resolver problemas complexos.
• Introduzir não‑linearidade nos neurônios, permitindo que redes profundas capturem padrões complexos e façam classificações em múltiplas classes.

GELU (Gaussian Error Linear Unit)

---

• Presente nas arquiteturas GPT-2/3
• Definição matemática: $\text{GELU}(x) = x \cdot \Phi(x)$, onde $\Phi(x)$ é a função de distribuição acumulada da normal padrão.
• Propriedades:
  • Se comporta como identidade para valores positivos (mantém quase todos os sinais).
  • Para valores negativos, atenua suavemente o valor em vez de cortá‑lo abruptamente como ReLU.
• Aproximação prática (usada na maioria das implementações):
  $$ \text{GELU}(x) \approx 0.5\,x\,[1 + \tanh(\sqrt{\frac{2}{\pi}}(x + 0.044715x^{3}))] $$
• Evita o cálculo direto de funções exponenciais, reduzindo a carga computacional.

class GELU(nn.Module):
    def __init__(self):
        super().__init__()

    def forward(self, x):
        return 0.5 * x * (1 + torch.tanh(
            torch.sqrt(torch.tensor(2.0 / torch.pi)) * 
            (x + 0.044715 * torch.pow(x, 3))
        ))

import matplotlib.pyplot as plt
import torch                       
import torch.nn as nn              

gelu, relu = nn.GELU(), nn.ReLU()

# Cria dados simples para plotar as funções
x = torch.linspace(-3, 3, 100)
y_gelu, y_relu = gelu(x), relu(x)

GELU x RELU

O que acontece com os gradientes nas duas funções?

plt.figure(figsize=(8, 3))
for i, (y, label) in enumerate(zip([y_gelu, y_relu], ["GELU", "ReLU"]), 1):
    plt.subplot(1, 2, i)
    plt.plot(x, y)
    plt.title(f"{label} activation function")
    plt.xlabel("x")
    plt.ylabel(f"{label}(x)")
    plt.grid(True)

plt.tight_layout()
plt.show()

Rede Feed-Forward

---

Usamos GELU na implementação da camada Feed-Forward com duas camadas lineares.

class FeedForward(nn.Module):
    def __init__(self, cfg):
        super().__init__()
        self.layers = nn.Sequential(
            nn.Linear(cfg["emb_dim"], 4 * cfg["emb_dim"]), GELU(),
            nn.Linear(4 * cfg["emb_dim"], cfg["emb_dim"]),
        )

    def forward(self, x):
        return self.layers(x)

A camada Feed-Forward é crucial para melhorar a habilidade do modelo de generalizar os dados. Embora entrada e saída ambos tenham a mesma dimensionalidade, a camada escondida expande a dimensionalidade dos embeddings a um espaço dimensional muito maior.

Dimensionalidade dos Vetores. Fonte: Sebastian Raschka.

4. Conexões de Atalho (Residual Connections)

---

Propostas originalmente para mitigar os problemas do desaparecimento do gradiente. Ideia: Adicionar a saída de uma camada à saída de uma camada posterior, geralmente pulando (skipping) uma ou mais camadas no meio. Uma conexão atalho cria um caminho alternativo e mais curto para o gradiente fluir através da rede.

class SimpleDeepNeuralNetwork(nn.Module):
    def __init__(self, layer_sizes, use_shortcut):
        super().__init__()
        self.use_shortcut = use_shortcut
        self.layers = nn.ModuleList([
            nn.Sequential(
                nn.Linear(layer_sizes[0], layer_sizes[1]), GELU()),
            nn.Sequential(
                nn.Linear(layer_sizes[1], layer_sizes[2]), GELU()),
            nn.Sequential(
                nn.Linear(layer_sizes[2], layer_sizes[3]), GELU()),
            nn.Sequential(
                nn.Linear(layer_sizes[3], layer_sizes[4]), GELU()),
            nn.Sequential(
                nn.Linear(layer_sizes[4], layer_sizes[5]), GELU())
        ])

    def forward(self, x):
        for layer in self.layers:
            layer_output = layer(x)
            # Verifica se o atalho pode ser aplicado
            if self.use_shortcut and x.shape == layer_output.shape:
                x = x + layer_output
            else:
                x = layer_output
        return x

Gradientes sem conexões de atalho

layer_sizes = [3, 3, 3, 3, 3, 1]  

sample_input = torch.tensor([[1., 0., -1.]])

torch.manual_seed(123)
model_without_shortcut = SimpleDeepNeuralNetwork(
    layer_sizes, use_shortcut=False
)

print_gradients(model_without_shortcut, sample_input)

layers.0.0.weight has gradient mean of 0.00020173587836325169
layers.1.0.weight has gradient mean of 0.0001201116101583466
layers.2.0.weight has gradient mean of 0.0007152041071094573
layers.3.0.weight has gradient mean of 0.0013988735154271126
layers.4.0.weight has gradient mean of 0.005049645435065031

Gradientes com conexões de atalho

torch.manual_seed(123)
model_with_shortcut = SimpleDeepNeuralNetwork(
    layer_sizes, use_shortcut=True
)
print_gradients(model_with_shortcut, sample_input)

layers.0.0.weight has gradient mean of 0.22169791162014008
layers.1.0.weight has gradient mean of 0.20694106817245483
layers.2.0.weight has gradient mean of 0.32896995544433594
layers.3.0.weight has gradient mean of 0.2665732204914093
layers.4.0.weight has gradient mean of 1.3258540630340576

5. Bloco Transformer

---

Agora, combinamos os conceitos anteriores em um bloco transformer:

Visão Geral GPT-2. Fonte: Sebastian Raschka.

class TransformerBlock(nn.Module):
    def __init__(self, cfg):
        super().__init__()
        self.att = MultiHeadAttention(
            d_in=cfg["emb_dim"],
            d_out=cfg["emb_dim"],
            context_length=cfg["context_length"],
            num_heads=cfg["n_heads"], 
            dropout=cfg["drop_rate"],
            qkv_bias=cfg["qkv_bias"])
        self.ff = FeedForward(cfg)
        self.norm1 = LayerNorm(cfg["emb_dim"])
        self.norm2 = LayerNorm(cfg["emb_dim"])
        self.drop_shortcut = nn.Dropout(cfg["drop_rate"])

    def forward(self, x):
        # Shortcut connection for attention block
        shortcut = x
        x = self.norm1(x)
        x = self.att(x)  # Shape [batch_size, num_tokens, emb_size]
        x = self.drop_shortcut(x)
        x = x + shortcut  # Adiciona a entrada original de volta
        
        shortcut = x # Conexão de atalho
        x = self.norm2(x)
        x = self.ff(x)
        x = self.drop_shortcut(x)
        x = x + shortcut  # Adiciona a entrada original de volta

        return x

torch.manual_seed(123)

x = torch.rand(2, 4, 768)  # Shape: [batch_size, num_tokens, emb_dim]
block = TransformerBlock(GPT_CONFIG_124M)
output = block(x)

print("Input shape:", x.shape)
print("Output shape:", output.shape)

Input shape: torch.Size([2, 4, 768])
Output shape: torch.Size([2, 4, 768])

6. Modelo GPT

• Vamos integrar o bloco Transformer na arquitetura GPT e montar uma versão totalmente funcional da versão original de 124 milhões de parâmetros do GPT-2.
• Tokenização e Embeddings: O texto tokenizado é convertido em embeddings de tokens, que são então combinados com embeddings posicionais.
• Empilhamento de Blocos Transformadores: O tensor resultante é processado por uma série de 12 blocos transformadores empilhados, cada um contendo camadas de atenção multi-cabeça e redes neurais feed forward com dropout e normalização de camada.

class GPTModel(nn.Module):
    def __init__(self, cfg):
        super().__init__()
        self.tok_emb = nn.Embedding(
            cfg["vocab_size"], cfg["emb_dim"])
        self.pos_emb = nn.Embedding(
            cfg["context_length"], cfg["emb_dim"])
        self.drop_emb = nn.Dropout(cfg["drop_rate"])
        self.trf_blocks = nn.Sequential(
            *[TransformerBlock(cfg) for _ in range(cfg["n_layers"])])
        self.final_norm = LayerNorm(cfg["emb_dim"])
        self.out_head = nn.Linear(
            cfg["emb_dim"], cfg["vocab_size"], bias=False
        )

    def forward(self, in_idx):
        batch_size, seq_len = in_idx.shape
        tok_embeds = self.tok_emb(in_idx)
        pos_embeds = self.pos_emb(
            torch.arange(seq_len, device=in_idx.device))
        # Shape [batch_size, num_tokens, emb_size]
        x = tok_embeds + pos_embeds
        x = self.drop_emb(x)
        x = self.trf_blocks(x)
        x = self.final_norm(x)
        logits = self.out_head(x)
        return logits

Saída do Modelo GPT

O tensor de saída tem a forma [2, 4, 50257], já que passamos 2 textos de entrada com 4 tokens cada. A última dimensão, 50257, corresponde ao tamanho do vocabulário do tokenizador. Abaixo veremos como converter cada um desses vetores de saída 50257-dimensional de volta para tokens.

torch.manual_seed(123)

model = GPTModel(GPT_CONFIG_124M)
out = model(batch)
batch.shape

print("Input batch:\n", batch)
print("\nOutput shape:", out.shape)
print(out)

Input batch:
 tensor([[6109, 3626, 6100,  345],
        [6109, 1110, 6622,  257]])

Output shape: torch.Size([2, 4, 50257])
tensor([[[ 0.3613,  0.4223, -0.0711,  ...,  0.3483,  0.4661, -0.2838],
         [-0.1792, -0.5660, -0.9485,  ...,  0.0477,  0.5181, -0.3168],
         [ 0.7120,  0.0332,  0.1085,  ...,  0.1018, -0.4327, -0.2553],
         [-1.0076,  0.3418, -0.1190,  ...,  0.7195,  0.4023,  0.0532]],

        [[-0.2564,  0.0900,  0.0335,  ...,  0.2659,  0.4454, -0.6806],
         [ 0.1230,  0.3653, -0.2074,  ...,  0.7705,  0.2710,  0.2246],
         [ 1.0558,  1.0318, -0.2800,  ...,  0.6936,  0.3205, -0.3178],
         [-0.1565,  0.3926,  0.3288,  ...,  1.2630, -0.1858,  0.0388]]],
       grad_fn=<UnsafeViewBackward0>)

Número de Parâmetros

O modelo tem 163M, e não 124M parâmetros

Amarração de pesos (weight tying): compartilhamento de pesos que é usado na arquitetura original do GPT-2, o que significa que a arquitetura original do GPT-2 está reutilizando os pesos da camada de embedding de token (tok_emb) em sua camada de saída, definindo assim self.out_head.weight = self.tok_emb.weight.

total_params = sum(p.numel() for p in model.parameters())
print(f"Total number of parameters: {total_params:,}")

Total number of parameters: 163,009,536

Número de Parâmetros (cont.)

Como podemos ver com base nas saídas de impressão, os tensores de peso para ambas essas camadas têm a mesma forma.

print("Token embedding layer shape:", model.tok_emb.weight.shape)
print("Output layer shape:", model.out_head.weight.shape)

Token embedding layer shape: torch.Size([50257, 768])
Output layer shape: torch.Size([50257, 768])

Número de Parâmetros (cont.)

Vamos remover a contagem de parâmetros da camada de saída da contagem total do modelo GPT-2, de acordo com a amarração de pesos:

out_head_params = sum(
    p.numel() for p in model.out_head.parameters())

total_params_gpt2 =  total_params - out_head_params

print(f"Params. treináveis (weight tying): {total_params_gpt2:,}")

Params. treináveis (weight tying): 124,412,160

Consumo de memória

A amarração de pesos reduz a pegada geral de memória e a complexidade computacional do modelo. No entanto, o uso de camadas separadas de embedding de token e saída resulta em melhor treinamento e desempenho do modelo.

Podemos calcular os requisitos de memória do modelo da seguinte forma:

# Calcula o tamanho total em bytes 
# (assumindo float32, 4 bytes por parâmetro)
total_size_bytes = total_params * 4
# Converte para megabytes
total_size_mb = total_size_bytes / (1024 * 1024)
print(f"Tamanho total do modelo: {total_size_mb:.2f} MB")

Tamanho total do modelo: 621.83 MB

7. Gerando Texto

---

Autoregessivo: Começando com um contexto de entrada inicial, o modelo estima um token subsequente em cada iteração, anexando-o ao contexto de entrada para a próxima rodada de previsão. O processo pelo qual um modelo GPT vai dos tensores de saída para o texto gerado envolve várias etapas que incluem decodificar os tensores de saída, selecionar tokens com base em uma distribuição de probabilidade e converter esses tokens em texto legível por humanos.

def generate_text_simple(model, idx, max_new_tokens, context_size):
    # idx é um array (batch, n_tokens) de índices no contexto atual
    for _ in range(max_new_tokens): # quantas tokens você quer gerar
        # Trunca o contexto atual se ele exceder 
        # o tamanho de contexto suportado
        # Ex: se LLM suporta apenas 5 tokens, 
        #  e o tamanho do contexto é 10 então 
        #  apenas os últimos 5 tokens são usados como contexto
        idx_cond = idx[:, -context_size:]
        
        with torch.no_grad():
            logits = model(idx_cond)
        
        # Foca apenas no último passo de tempo
        # (batch, n_tokens, vocab_size) se torna (batch, vocab_size)
        logits = logits[:, -1, :] 

        # Aplica softmax para obter probabilidades
        probas = torch.softmax(logits, dim=-1)  # (batch, vocab_size)

        # Obtém o idx do vocabulário com maior probabilidde
        idx_next = torch.argmax(probas, dim=-1, keepdim=True) 
        # argmax retorna a posição de índice do valor mais alto

        # Anexa o índice amostrado à sequência em execução
        idx = torch.cat((idx, idx_next), dim=1)  # (batch, n_tokens+1)

    return idx

Texto de Entrada (Contexto)

start_context = "Hello, I am"

encoded = tokenizer.encode(start_context)
print("encoded:", encoded)

encoded_tensor = torch.tensor(encoded).unsqueeze(0)
print("encoded_tensor.shape:", encoded_tensor.shape)

encoded: [15496, 11, 314, 716]
encoded_tensor.shape: torch.Size([1, 4])

Geração de Texto

Note que como não treinamos o modelo ainda, o resultado um texto sem sentido.

model.eval() # Desabilita dropout
out = generate_text_simple(
    model=model,
    idx=encoded_tensor, 
    max_new_tokens=6, 
    context_size=GPT_CONFIG_124M["context_length"]
)
print("Output:", out)
print("Output length:", len(out[0]))

decoded_text = tokenizer.decode(out.squeeze(0).tolist())
print(decoded_text)

Output: tensor([[15496,    11,   314,   716, 27018, 24086, 47843, 30961, 42348,  7267]])
Output length: 10
Hello, I am Featureiman Byeswickattribute argue

Próximos Passos

• Experimentar com Pre-LN x Post-LN.
• Modifique as configurações do modelo GPT-2 implementado aqui.
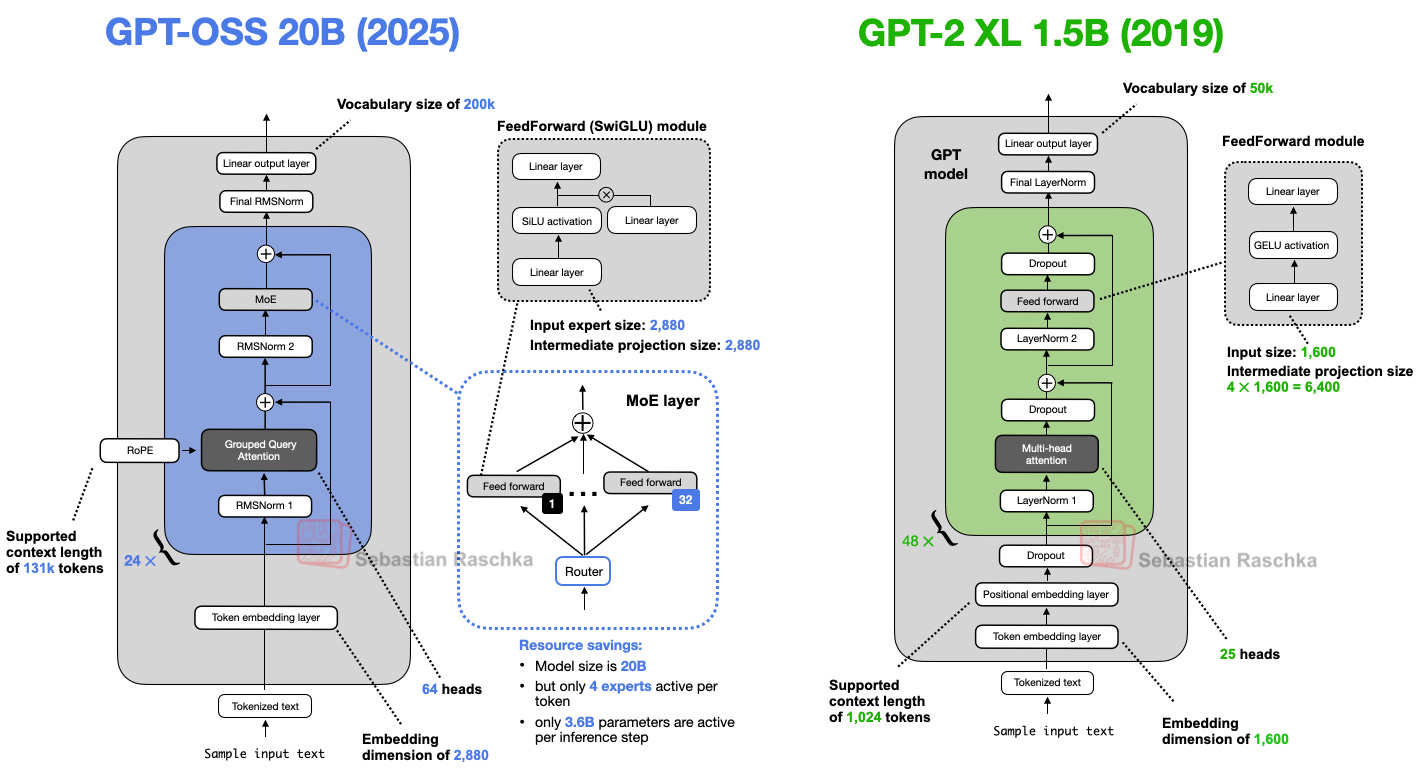
• Analisar as diferenças entre GPT-2 e modelos mais modernos como o GPT-OSS.