Adjacência
- Adjacência: Dois pixels são adjacentes se compartilham pelo menos um ponto comum (contorno ou vértice).
- 4‑adjacência – vizinhos que compartilham uma borda:
- 8‑adjacência – inclui também os quatro diagonais:
- 4‑adjacência – vizinhos que compartilham uma borda:
- Conectividade: Um conjunto de pixels forma uma região se cada pixel da região pode ser alcançado a partir de qualquer outro via um caminho de adjacentes dentro da mesma região.

Exemplo de adjacência de pixels. Fonte: Jackson Gomes.
Filtragem Espacial
- Ideia Geral: Cada pixel
- Objetivo principal: modificar características da imagem (suavizar, realçar bordas, remover ruído).
- Componente principal: Filtro aplicado sobre a imagem. Expresso como uma matriz ou, de forma análoga, como uma imagem.
- Nomenclatura: Filtros, Máscaras, Kernel:
- Nomenclatura: Filtros, Máscaras, Kernel:

Exemplo de aplicação de filtro de aguçamento e de suavização. Fonte: COVAP-UTFPR
Filtro Espacial
- Componentes:
- Vizinhança: normalmente um pequeno retângulo.
- Operação: realizada sobre os pixels da imagem incluídos na vizinhança.
- Filtragem: cria um novo pixel com coordenadas iguais às coordenadas do centro da vizinhança, e cujo valor é o resultado da operação de filtragem.
- Imagem Filtrada (ou processada): Gerada à medida que o centro do filtro percorre cada pixel na imagem de entrada.
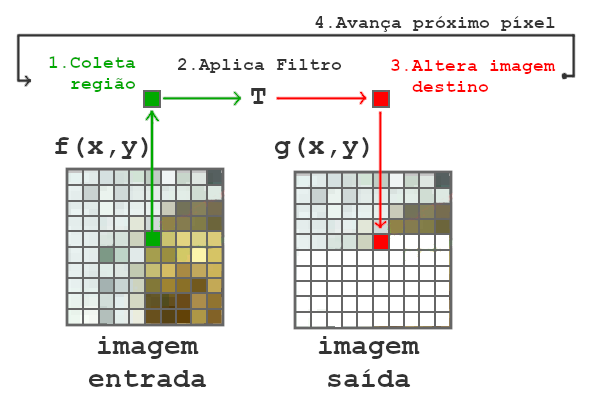
Esquema geral da filtragem espacial. Fonte: visaocomputacional.com.br.
Convolução
- Operação fundamental nesta disciplina.
- Kernel: matriz de pesos
- Duas representações geral de um kernel 3 x 3 na lousa
Operação de correlação onde as partes sombreadas são o primeiro elemento de saída, bem como os elementos tensores de entrada e kernel usados para o cálculo de saída. Fonte: Deep Dive into Deep Learning.
Convolução é a base para as CNNs,
redes neurais convolucionais,
e para deep learning.
Exemplo de Filtragem Espacial

Exemplo de aplicação de filtro espacial. Fonte: Cezanne Camacho.
Exercício Prático: Convolução
- Dados a imagem de entrada
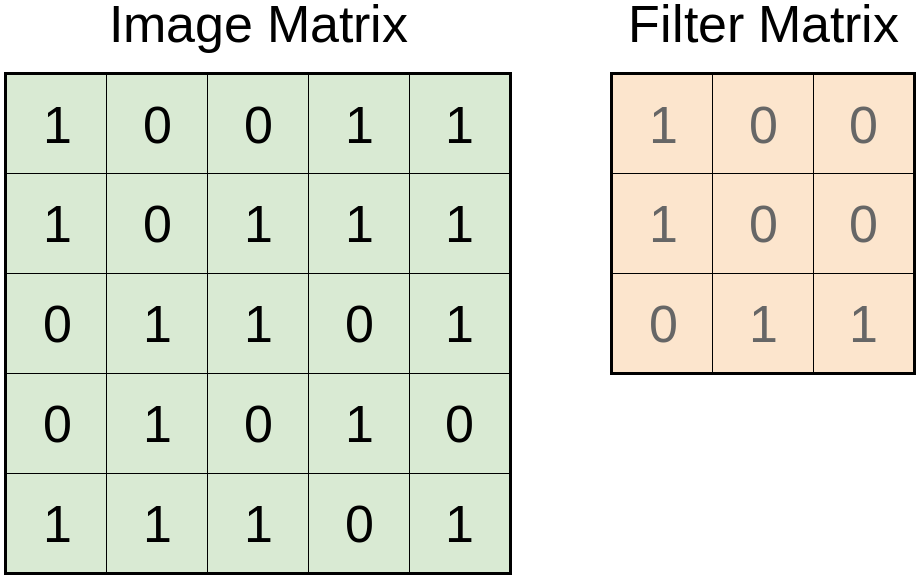
Exemplo de convolução. Fonte: Austing Walters.
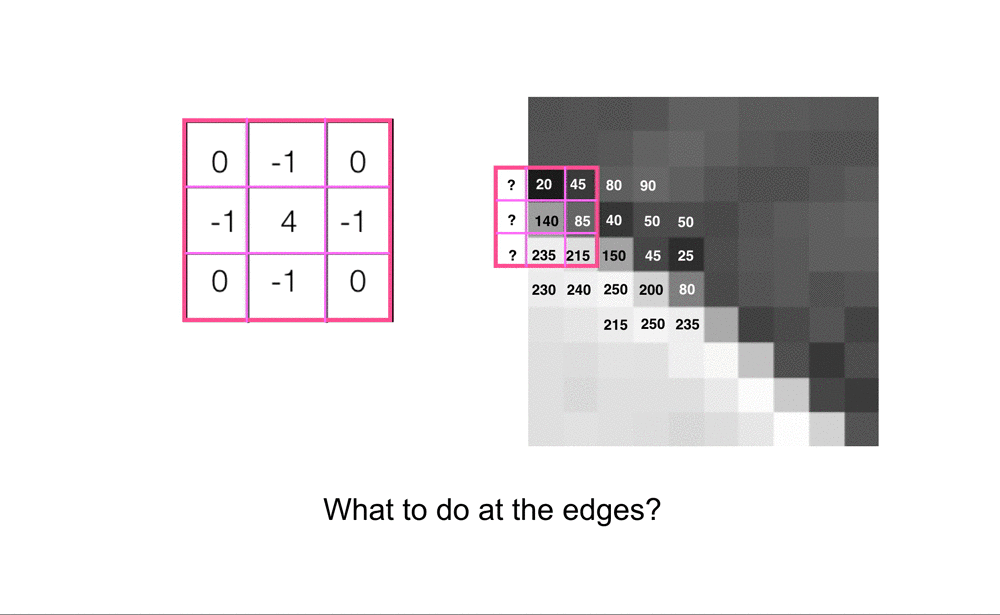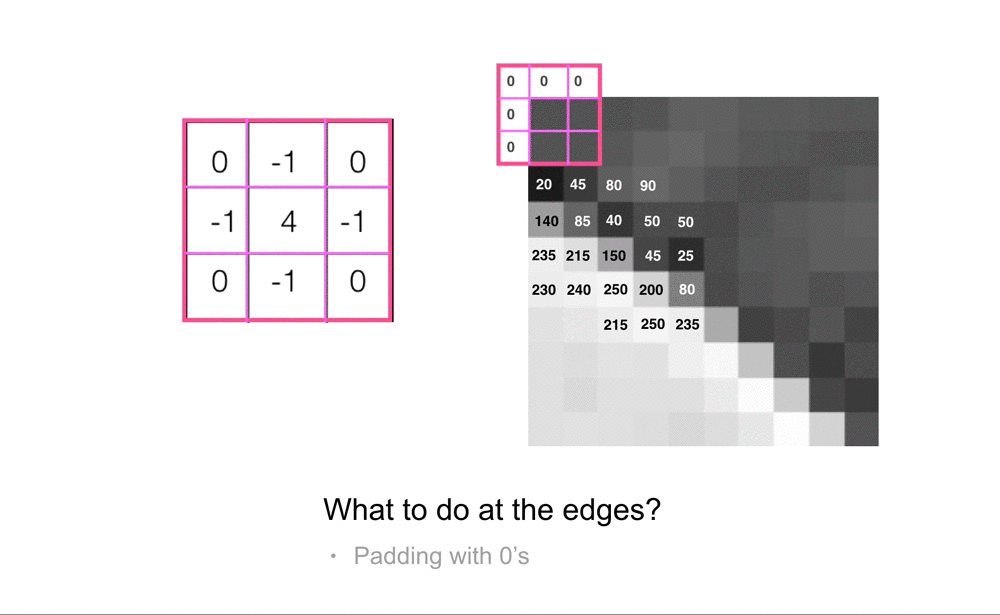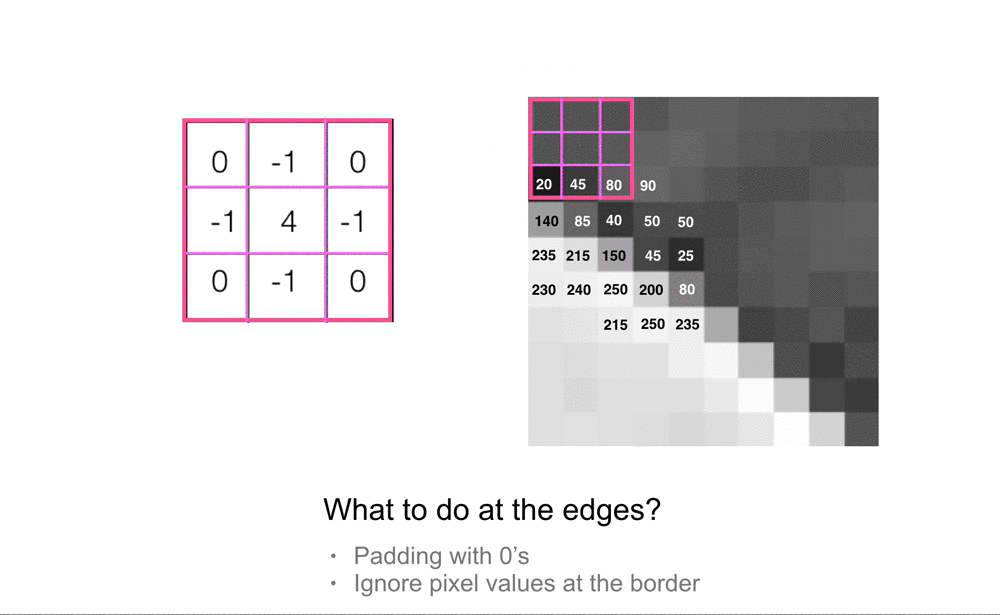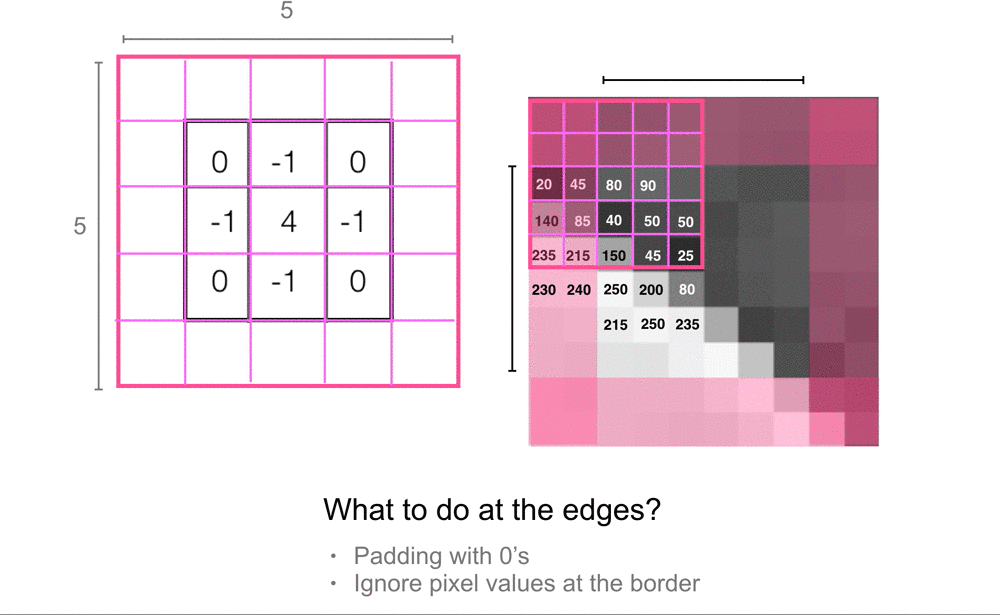
Convolução nas bordas de uma imagem. Fonte: Cezanne Camacho.
Exercício Prático: Convolução (Resolução)

Exemplo de convolução. Fonte: Austing Walters.
Implementação Prática (OpenCV)
import cv2
import numpy as np
# Carregar a imagem em escala de cinza
imagem = cv2.imread("exemplo.jpg", cv2.IMREAD_GRAYSCALE)
# Definir um kernel de suavização (média)
kernel = np.ones((3,3), np.float32) / 9 # Normalizamos dividindo por 9
# Aplicar a convolução com o kernel
imagem_suavizada = cv2.filter2D(imagem, -1, kernel)
# Mostrar as imagens original e suavizada
cv2.imshow("Original", imagem)
cv2.imshow("Suavizada", imagem_suavizada)
cv2.waitKey(0)
cv2.destroyAllWindows()
Exemplos de Filtros Espaciais
- Filtro de Média: Utilizado para suavização da imagem.
- Diminui a nitidez pela redução de fortes transições de intensidade entre os pixels.
- Desfocar os objetos menores e deixar os maiores em maior evidência.
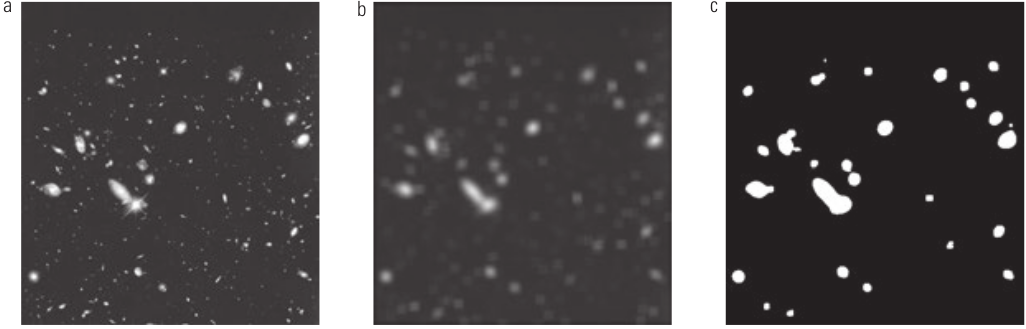
Exemplo de kernel de média 15 x 15 sobre uma imagem capturada pelo telescópio Hubble. Note que o desfoque ajuda a dar mais ênfase aos objetos maiores. A terceira imagem é o resultado de thresholding. Fonte: COVAP-UTFPR.

Exemplo de aplicação de filtro de média.
Filtros quadrados de tamanhos 3, 5, 9, 15 e 35. Fonte: COVAP-UTFPR
Exemplos de Filtros Espaciais (cont.)
- Filtro de Mediana: Utilizado para redução de ruído da imagem.
- Elimina picos isolados (outliers).
- Substitui o valor de um pixel pela mediana dos valores de intensidade na vizinhança desse pixel.
- Note que o valor original do pixel é incluído no cálculo da mediana.

Exemplo de remoção de ruído sal e pimenta em imagem de raio X de uma placa de circuito por filtro de mediana. Fonte: COVAP-UTFPR.
Filtro Gaussiano
- Filtro de média ponderada, mas com seus pesos seguindo uma aproximação da distribuição gaussiana.
- Suaviza a imagem (leve borramento), mas preserva melhor as bordas.
- Indicado para reduzir ruído branco e no pré‑processamento em detecção de bordas.
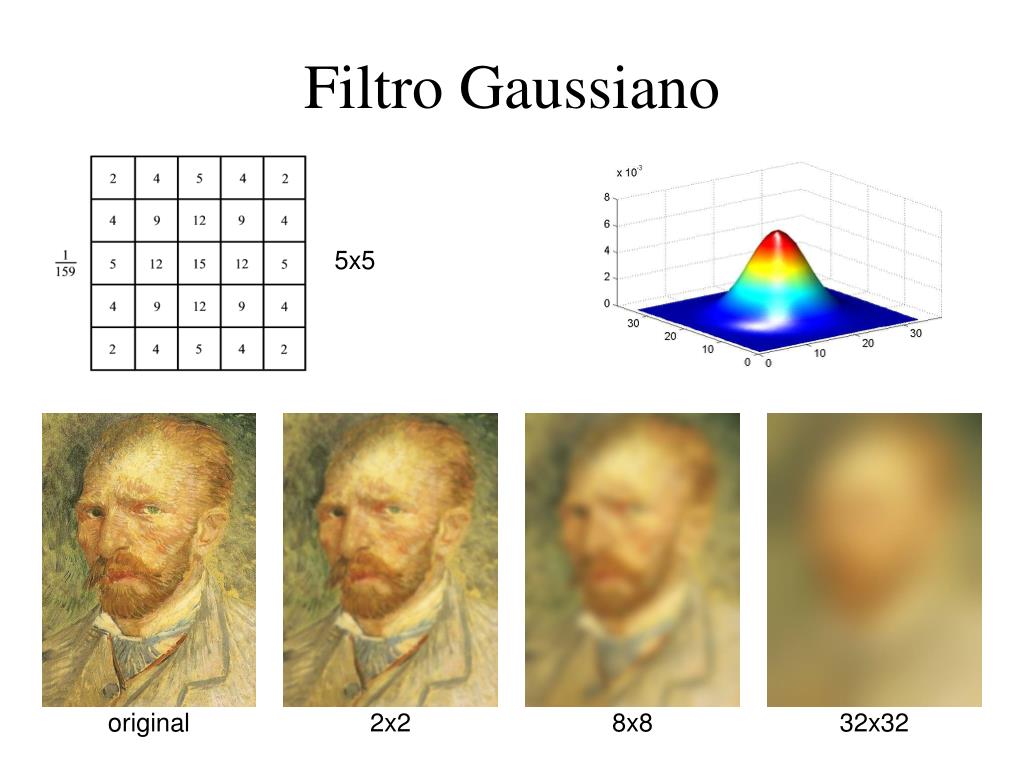
Aplicação de filtro gaussiano de diferentes tamanhos. Fonte: Slide Serve.
Outros de Filtros Espaciais
Imagem Original (identidade)

Detecção de Borda

Exemplo de filtros espaciais. Fonte: COVAP-UTFPR.
Filtro Laplaciano
Detecta variação de intensidade (bordas).
Filtro de Sobel
Estima gradientes em direções horizontal e vertical.
Demonstração em https://setosa.io/ev/image-kernels/
Classificação de Filtros
- Lineares – resposta proporcional à entrada (ex.: convolução).
- Não‑lineares – dependência de funções não lineares (ex.: mediana).
| Tipo | Operação principal | Exemplo |
|---|---|---|
| Linear | Média, Gaussiano | |
| Não‑linear | Função de decisão sobre vizinhança | Max, Mediana |
Extra: Dilatação e Erosão
Dilatação
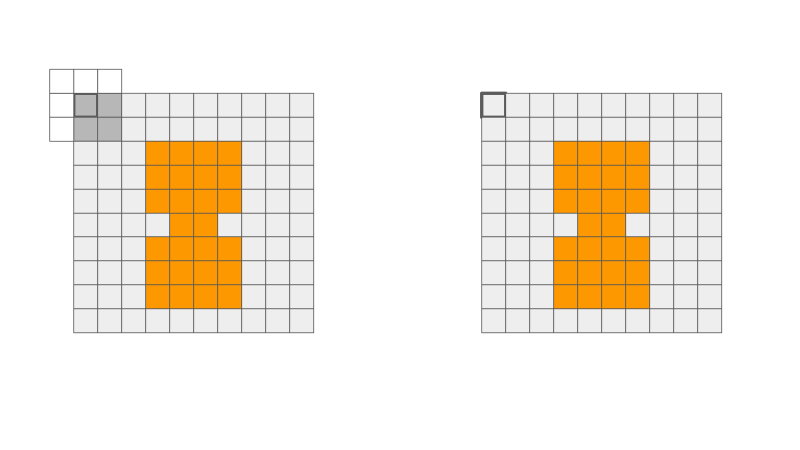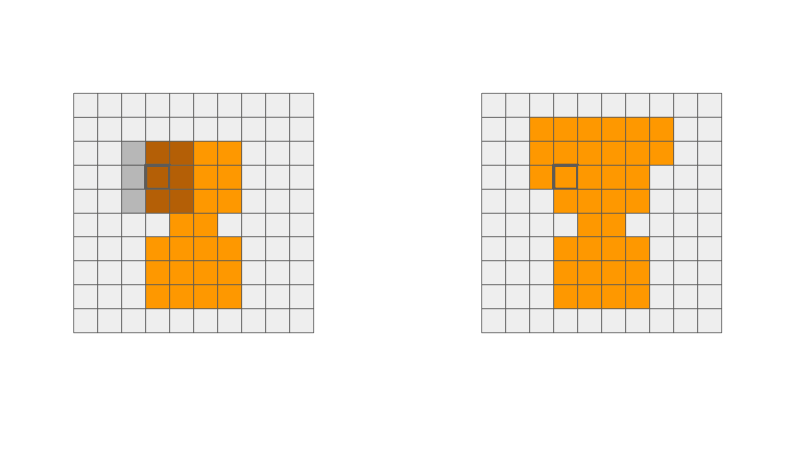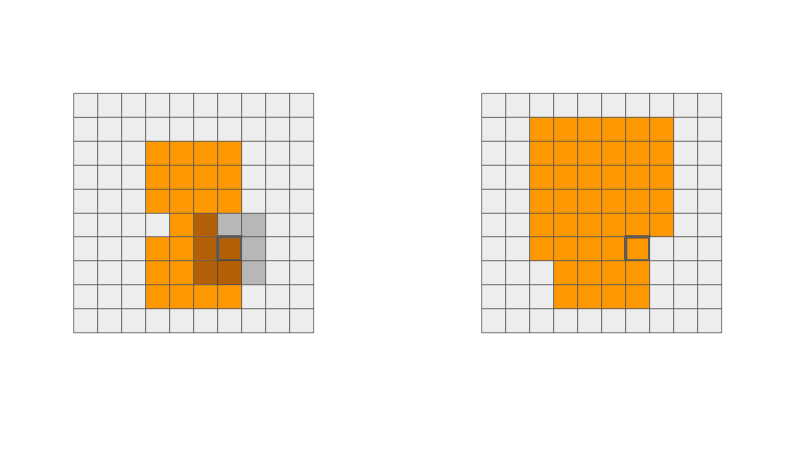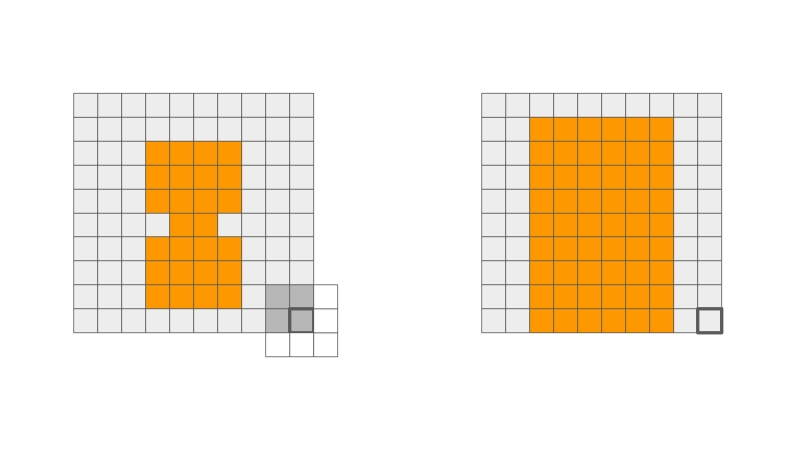
Erosão
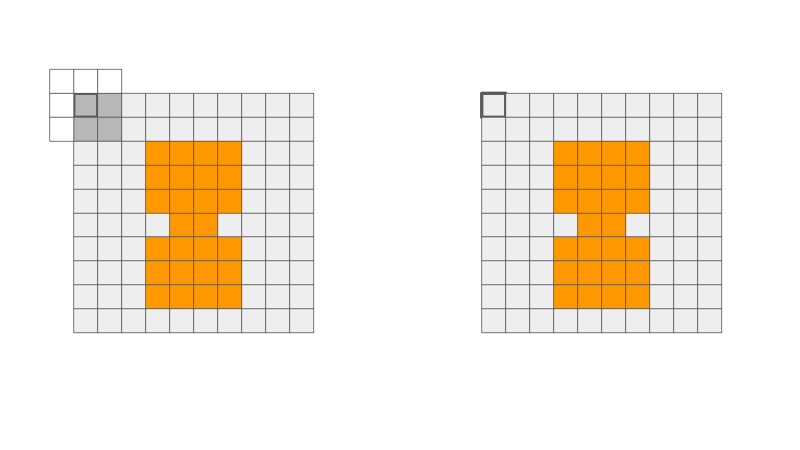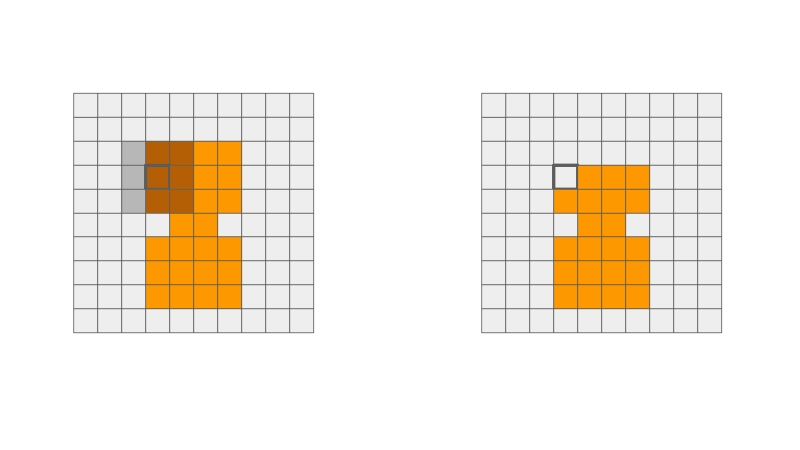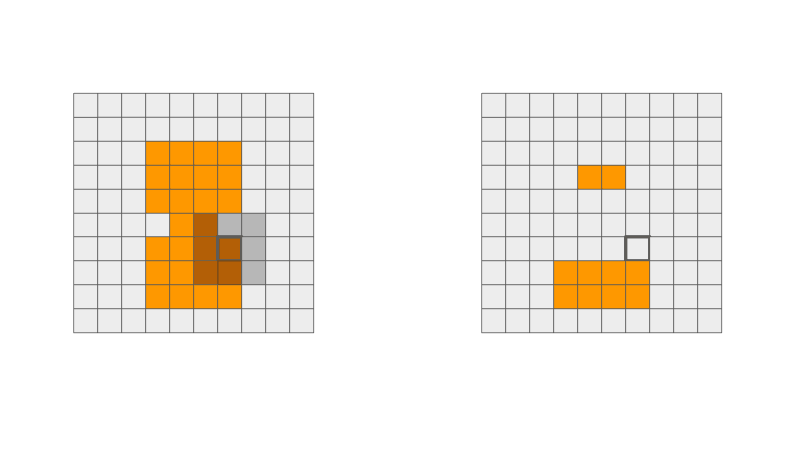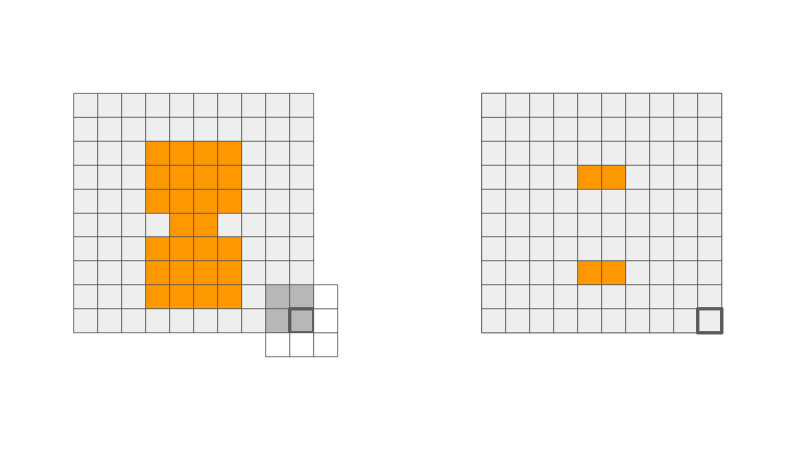
Ilustração de operação de dilatação e erosão via filtros espaciais. Fonte: Penny Xu.
Resumo e Próximos Passos
- Convolução: ferramenta matemática central.
- Filtros lineares (média, Gaussiano) oferecem suavização controlada; a separabilidade do kernel pode reduzir drasticamente o custo computacional.
- Filtros não‑lineares (mediana, adaptativos) são essenciais para robustez contra ruído impulsivo e preservação de bordas em cenários adversos.
- A escolha entre suavização e realce depende da aplicação: imagens médicas, visão robótica ou processamento de vídeo em tempo real.
- Próximos passos: Implementar filtros e analisar resultados (prática).

Atividade recomendada: Leitura das seções 3.4 a 3.7.
Perguntas e Discussão
- Cite três aplicações industriais ou científicas onde a filtragem espacial desempenha um papel crítico e explique por que o filtro escolhido foi adequado ao problema.
- Como você aplicaria filtros espaciais para melhorar a qualidade de imagens médicas (ex.: tomografia, ressonância magnética) sem introduzir artefatos que possam comprometer o diagnóstico?
- Quais são as principais limitações dos filtros lineares quando se trata de preservar detalhes finos em imagens de alta resolução?
- Como os filtros não‑lineares, como a mediana, podem alterar a distribuição de intensidade da imagem e quais implicações isso tem para tarefas subsequentes (segmentação, classificação)?
