Visão Computacional¶
Estratégias para Reduzir Overfitting¶
Prof. Dr. Denis Mayr Lima Martins¶
Pontifícia Universidade Católica de Campinas¶

Objetivos de Aprendizagem¶
- Compreender como modificação da função objetivo pode prevenir o overfitting.
- Analisar Estratégias de Normalização (Input Norm e BatchNorm) e Inicialização de Peso (Xavier) para garantir um fluxo de gradientes saudável em redes profundas.
- Utilizar Data Augmentation (aumento de dados) através da expansão artificial do conjunto de treinamento
- Gerenciar o Ciclo de Treinamento com Critérios de Validação (Early Stopping), determinando o ponto ótimo de parada com base no monitoramento do erro no conjunto de validação.
Regularização¶
- Regularização modifica a função objetivo para adicionar uma penalidade contra a complexidade, visando reduzir a variância e a capacidade do modelo.
- Forma geral: adicionar penalidades à função de loss para desencorajar que os pesos atinjam valores excessivamente grandes.
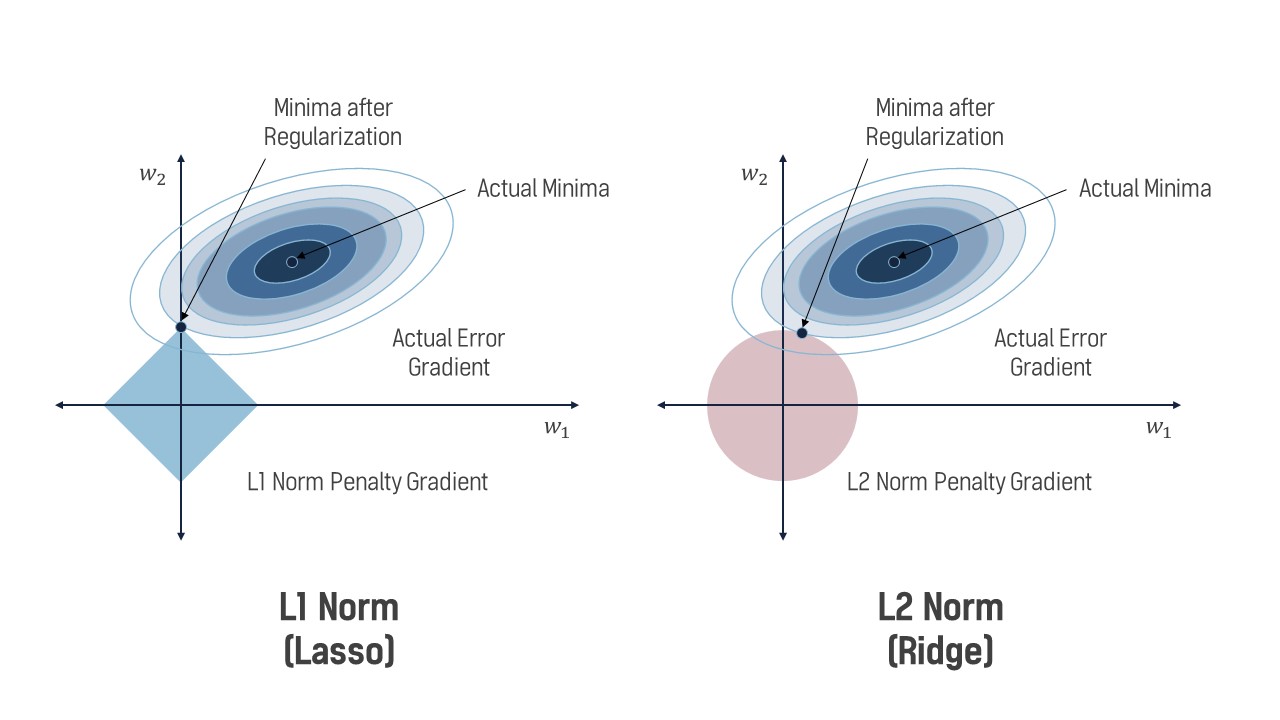
- L1 (LASSO): Usa a norma $||\mathrm{w}||$ (soma dos valores absolutos dos pesos).
- L2 (Ridge): Usa a norma $||\mathrm{w}||_2^2$ (soma dos quadrados dos pesos).
Regularização L1 (exemplo)¶
for data, target in data_loader:
optimizer.zero_grad()
output = model(data)
loss = loss_function(output, target)
# L1 regularization
l1_lambda = 0.001
l1_norm = sum(torch.abs(param).sum() for param in model.parameters())
# Combina o termo da L1 reg com a loss original
total_loss = loss + l1_lambda * l1_norm
total_loss.backward()
optimizer.step()
Regularização L2 (exemplo)¶
LAMBDA = 0.01
optimizer = torch.optim.SGD(
model.parameters(),
lr=0.1,
weight_decay=LAMBDA
)
|
 Efeito da Regularização L2. Fonte: Ha-Yoon Song.
Efeito da Regularização L2. Fonte: Ha-Yoon Song.
|
Regularização L1 e L2¶
Regularização L1 e L2¶
Dropout¶
|
 Efeito de Dropout. Fonte: Research Gate.
Efeito de Dropout. Fonte: Research Gate.
|
Dropout¶
class CNNWithDropout(nn.Module):
def __init__(self):
super(CNNWithDropout, self).__init__()
self.my_network = torch.nn.Sequential(
# ... Camada Linear ...
torch.nn.ReLU(),
torch.nn.Dropout(drop_proba),
# ...
)
Normalização para Estabilização do Treinamento¶
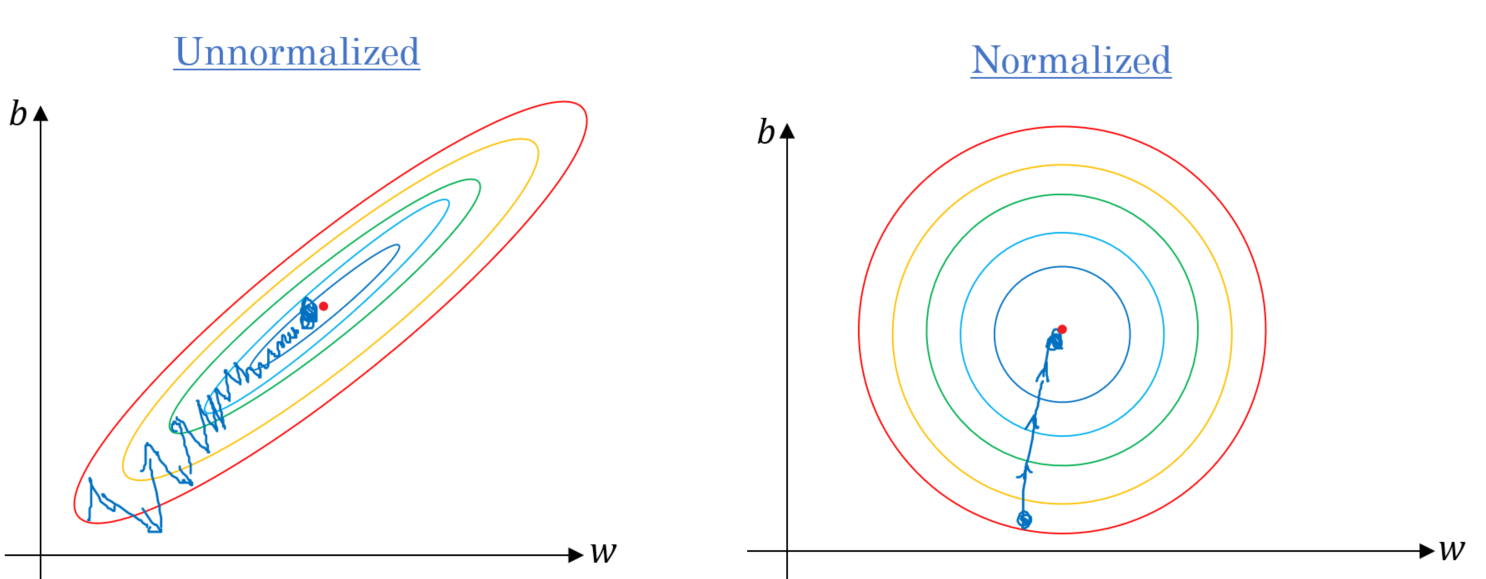
Input Normalization: Normalizar as features de entrada é um passo inicial crucial para o Gradiente Descendente, garantindo que todas as características tenham zero média e unidade de variância (standardization).
Normalização para Estabilização do Treinamento¶
|
Batch Normalization (BatchNorm): Propõe estender a normalização para as entradas das camadas ocultas. A BatchNorm ajuda a lidar com os problemas de gradientes explosivos/desvanecentes e melhora a estabilidade e a taxa de convergência do treinamento. Exemplo: self.conv1 = nn.Conv2d(3, 16, kernel_size=3, padding=1)
self.bn1 = nn.BatchNorm2d(16)
self.relu = nn.ReLU()
|
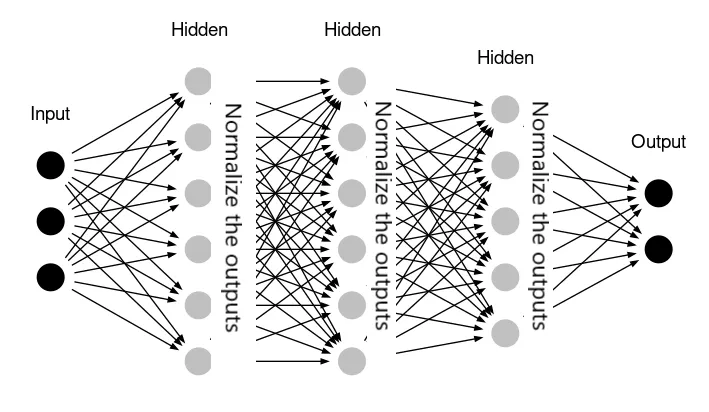 BatchNorm em MLP. Fonte: Ilango Rajagopal.
BatchNorm em MLP. Fonte: Ilango Rajagopal.
|
BatchNorm¶
Seja uma net input $z^{[i]}_j$ do exemplo $i$ para o neurônio $j$ no minibatch de tamanho $n$:
- Passo 1 (Cálculo de Média e Variância): $\mu_j = \frac{1}{n} \sum_{i} z^{[i]}_j \quad \sigma^2_j = \frac{1}{n} \sum_{i} (z^{[i]}_j - \mu_j)^2$
- Passo 2 (Normalização): $z'^{[i]}_j = \frac{z^{[i]}_j - \mu_j}{\sqrt{\sigma^2_j + \epsilon}}$
- Passo 3 (Pre-Activation Scaling): $a'^{[i]}_j = \gamma_j \cdot z'^{[i]}_j + \beta_j$
- $\gamma_j$ (controla a escala/dispersão)
- $\beta_j$ (controla a média) são parâmetros aprendíveis.
 Efeito da BatchNorm. Fonte: Towards Data Science.
Efeito da BatchNorm. Fonte: Towards Data Science.
Early Stopping¶
- Modelos complexos tendem a ter um desempenho de generalização (validação) que melhora inicialmente e depois se degrada à medida que o overfitting começa.
- O Early Stopping é uma estratégia de regularização que envolve parar o treinamento antes da convergência total no conjunto de treinamento.
- Critério: O treinamento é interrompido quando a métrica de desempenho no conjunto de validação (geralmente a perda de validação) para de melhorar ou começa a piorar significativamente por um número de épocas pré-definido (patience).
Data Augmentation¶
- Gerar artificialmente mais dados de treinamento a partir do conjunto existente. Isso é frequentemente a melhor maneira de reduzir o overfitting quando não é viável coletar mais dados reais.
- Aumento de dados injeta invariância e robustez ao modelo, expondo-o a variações que preservam a classe, como: Flip (Inversão Horizontal), Crop (Corte Aleatório), Color Jitter (Aumento de cor/brilho), Rotation (Rotação Aleatória), etc.
 Exemplos de Data Augmentation. Fonte: UniData.
Exemplos de Data Augmentation. Fonte: UniData.
Data Augmentation (exemplo)¶
training_transforms = torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Resize(32, 32),
torchvision.transforms.RandomCrop(28, 28),
torchvision.transforms.RandomRotation(degrees=30),
torchvision.transforms.Normalize(mean=(0.5), std=(0.5))
])
Inicialização de Pesos¶
- Uma inicialização inadequada dos pesos pode levar a problemas de gradientes desvanecentes/explosivos (Vanishing/Exploding Gradient Problems), especialmente em redes profundas. Inicialmente, buscava-se usar pequenos números aleatórios para quebrar a simetria.
- Inicialização Xavier/Glorot: Proposta para funções de ativação como $\text{TanH}$. O método escala os pesos em proporção ao número de entradas na camada (fan in).
- Inicialização He/Kaiming: Desenvolvida para ativações ReLU. PyTorch utiliza o esquema Kaiming He por padrão.
- Leitura Recomendada: A Gentle Introduction To Weight Initialization for Neural Networks
Para uma intuição visual sobre o efeito da inicialização dos parâmetros, veja: https://www.deeplearning.ai/ai-notes/initialization/index.html
Resumo¶
|
 Leitura Recomendada: Capítulo 7.
Leitura Recomendada: Capítulo 7.
|
Perguntas e Discussão¶
- Qual é a diferença fundamental no mecanismo de combate ao overfitting entre a Regularização L1/L2 (penalidade de norma, forçando pesos menores) e o Dropout (desativação estocástica de neurônios, prevenindo a co-adaptação)? Em que cenários cada abordagem tende a ser mais eficaz?
- A Normalização de Batch (BatchNorm) provou ser um método robusto para estabilizar o treinamento e acelerar a convergência. Discuta como a BatchNorm reduz a dependência de esquemas precisos de inicialização de pesos (como He ou Xavier) e por que a inicialização ainda permanece relevante, mesmo com a presença de BatchNorm.
- Se as curvas de treinamento e validação de um modelo divergem significativamente (indicando alta variância/overfitting), como um engenheiro de Deep Learning decidiria a ordem de prioridade entre: a) aumentar a Regularização L2, b) aumentar a complexidade do pipeline de Data Augmentation, e c) reduzir a paciência do Early Stopping?