Visão Computacional¶
Gradiente Descendente e Backpropagation¶
Prof. Dr. Denis Mayr Lima Martins¶
Pontifícia Universidade Católica de Campinas¶

Recap: Uma CNN é apenas uma grande equação¶
Considere o esboço de equação de uma CNN: $$\,z_k = \sum_{j=1}^{D}\! \Bigl[W^{(\ell)}_{jk} \,\bigl( \operatorname{flatten} \!\bigl( \text{pool}\!\bigl( \phi\!\bigl( \operatorname{conv}(x;W^{(c)})+b^{(c)} \bigr) \bigr) \bigr)\bigr)_j \Bigr] + b^{(\ell)}_k $$
- Durante o treinamento, precisamos ajustar cada parâmetro da CNN de forma a diminuir o erro da rede.
- O problema principal do treinamento é a otimização dos parâmetros da rede.
Objetivos de Aprendizagem¶
- Conceituar e Aplicar a otimização de funções de custo em Deep Learning.
- Descrever as variantes do algoritmo Gradient Descent.
- Compreender e Derivar o funcionamento de Back-Propagation.
Motivação: O Desafio do Treinamento¶
O treinamento de um modelo de Deep Learning (DL) é um problema de otimização.
- Objetivo: Encontrar o conjunto de parâmetros ($\mathbf{w}, \mathbf{b}$) de uma rede neural que minimiza uma função de custo (ou perda) $\mathcal{L}$.
- A função de custo $\mathcal{L}(\mathbf{w}, \mathbf{b})$ mede o quão "ruim" o modelo $f(\mathbf{x};\mathbf{w}, \mathbf{b})$ é em mapear as entradas $\mathbf{x}$ para as saídas desejadas $\mathbf{y}$.
Onde $\boldsymbol{\phi}$ representa o vetor de todos os parâmetros $(\mathbf{w}, \mathbf{b})$ do modelo.
Função de Custo: O que estamos minimizando?¶
|
A função de custo mais comum, especialmente para problemas de regressão, é o Erro Quadrático Médio (MSE):
O Desafio: A função $\mathcal{L}$ geralmente é não-convexa para redes profundas, possuindo múltiplos mínimos locais e pontos de sela (saddle points). |
O Conceito de Gradiente ($\nabla\mathcal{L}$)¶
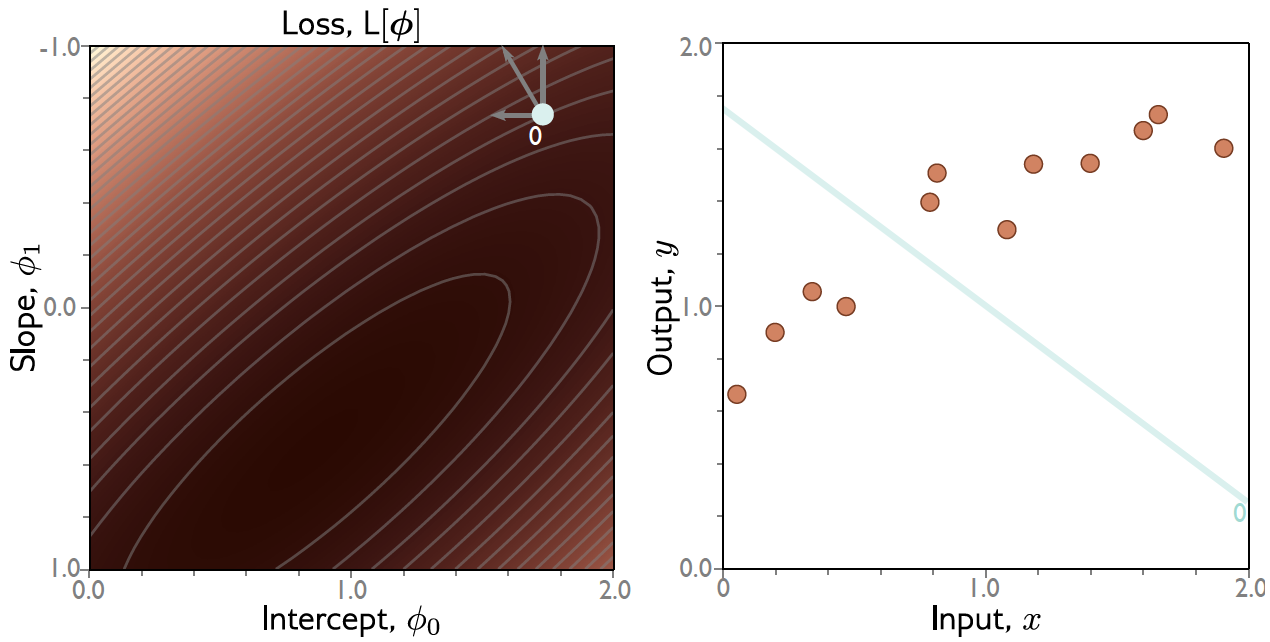
Para encontrar o ponto de mínimo de $\mathcal{L}(\mathbf{w})$, utilizamos o gradiente, que é um vetor de derivadas parciais.
- O gradiente $\nabla\mathcal{L}(\mathbf{w})$ aponta na direção de máximo crescimento da função.
- Portanto, o oposto do gradiente, $-\nabla\mathcal{L}(\mathbf{w})$, aponta na direção de descida mais íngreme (steepest descent).
Definição Matemática: O gradiente é o mapeamento que leva um vetor de parâmetros $\mathbf{w}$ a um vetor de derivadas parciais: $$ \nabla\mathcal{L} (\mathbf{w}) = \left( \frac{\partial\mathcal{L}}{\partial w_1}, \frac{\partial\mathcal{L}}{\partial w_2}, \dots, \frac{\partial\mathcal{L}}{\partial w_D} \right)^T $$
Veremos mais detalhes na lousa.
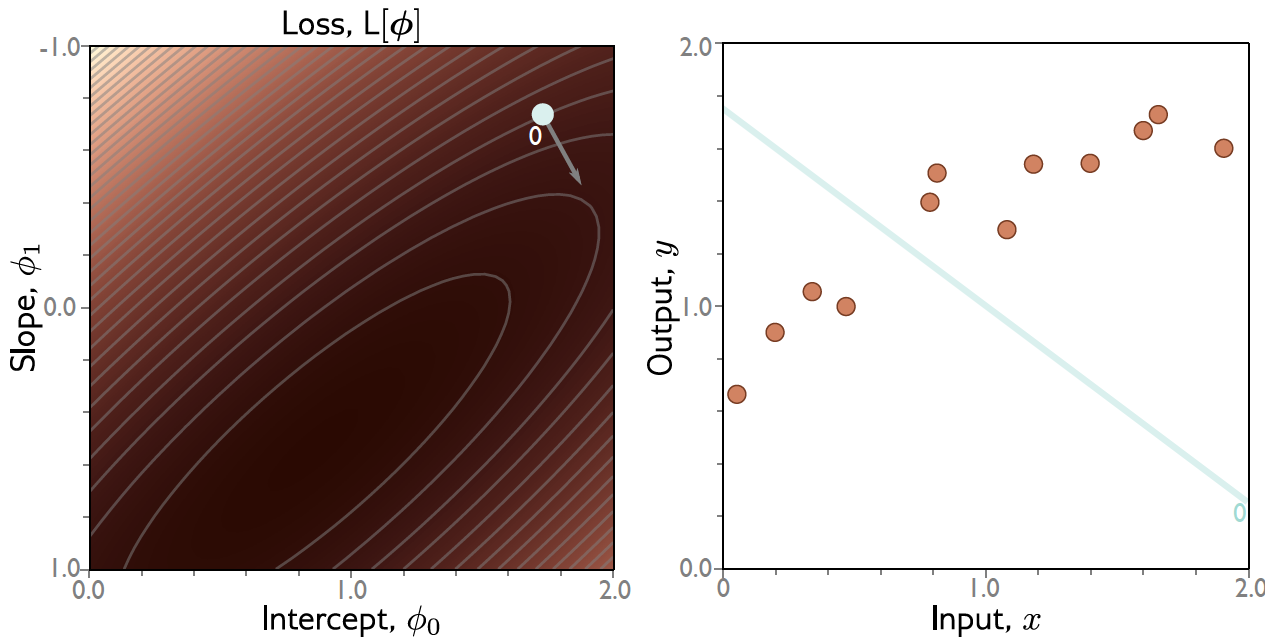
Gradient Descent¶
O algoritmo Gradient Descent (GD) é o método geral de minimização que usa informações lineares locais para mover-se iterativamente em direção a um mínimo (local).
O Algoritmo em 2 Passos:
- Cálculo: Calcule o gradiente da função de custo $\mathcal{L}$ em relação aos parâmetros $\mathbf{w}$.
- Atualização: Atualize os parâmetros dando um "passo" no sentido contrário ao gradiente (descida).
Fórmula de Atualização Central: $$ \mathbf{w}_{t+1} = \mathbf{w}_t - \eta \nabla\mathcal{L} (\mathbf{w}_t) $$
- Onde $\mathbf{w}_t$ são os parâmetros na iteração $t$, e $\eta > 0$ é a taxa de aprendizado ($\eta$ - learning rate), que controla o tamanho do passo.
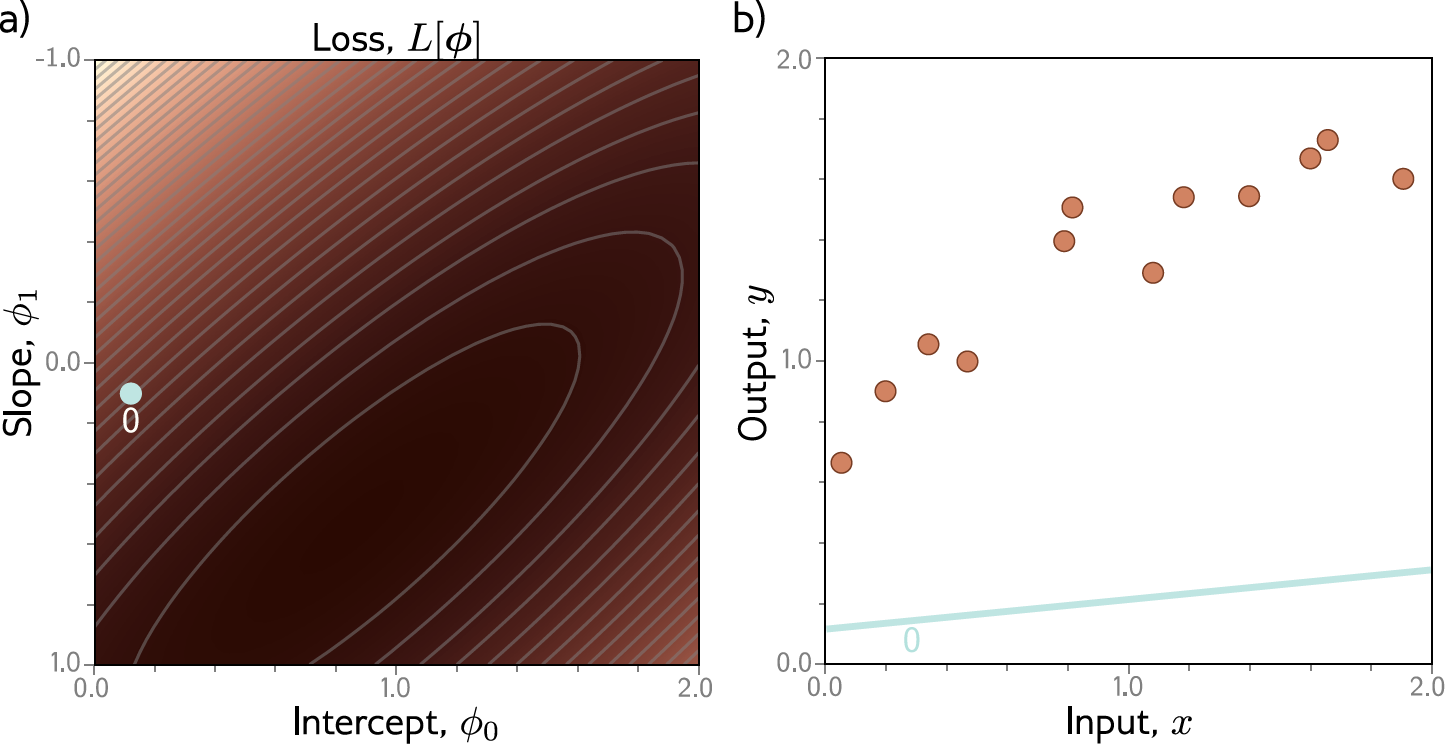
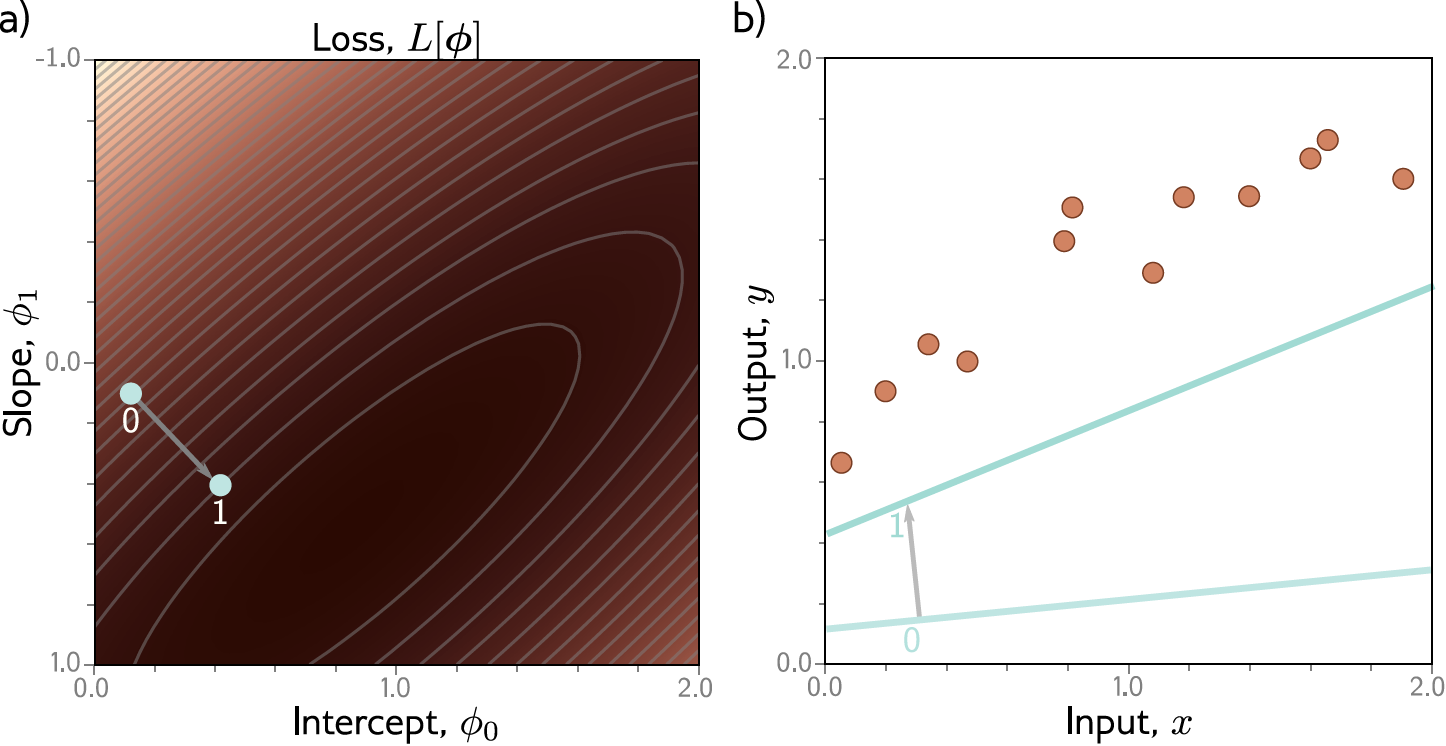
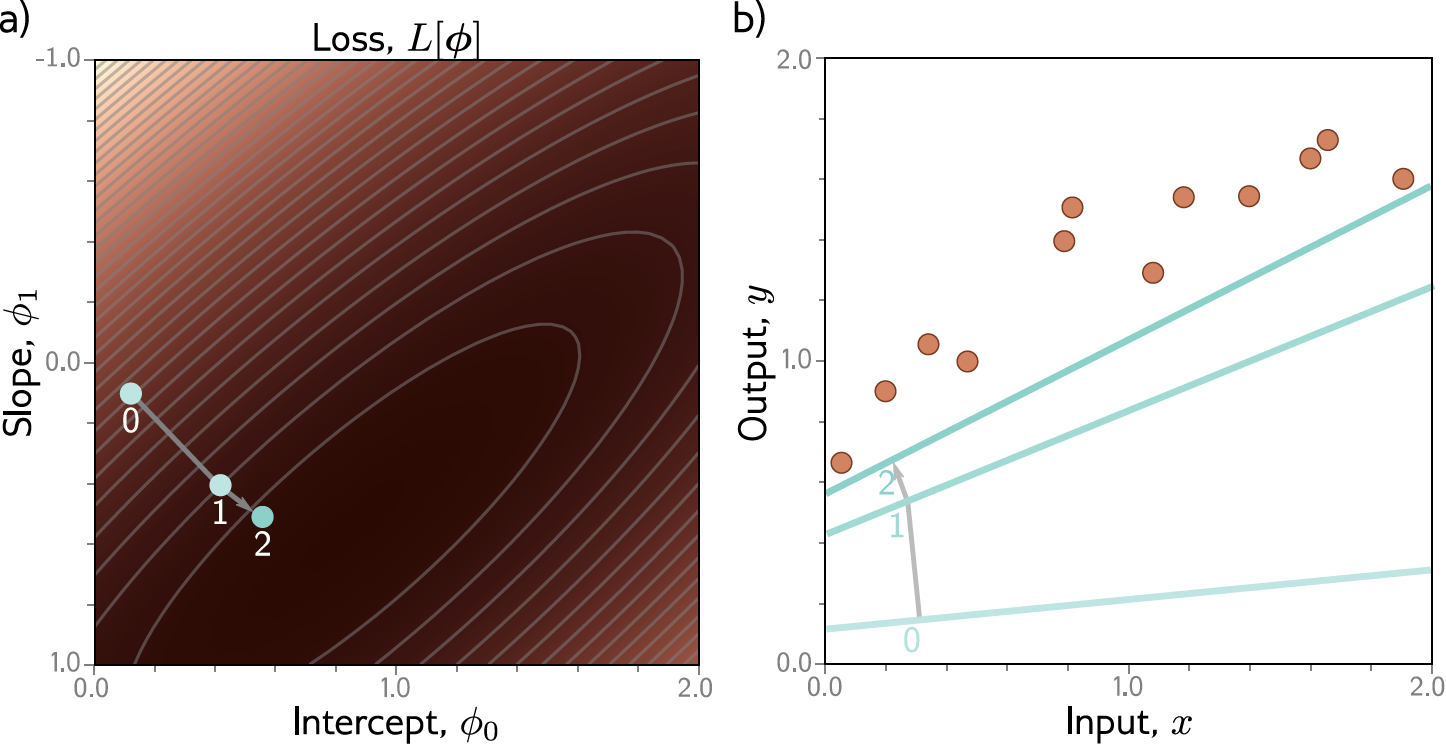
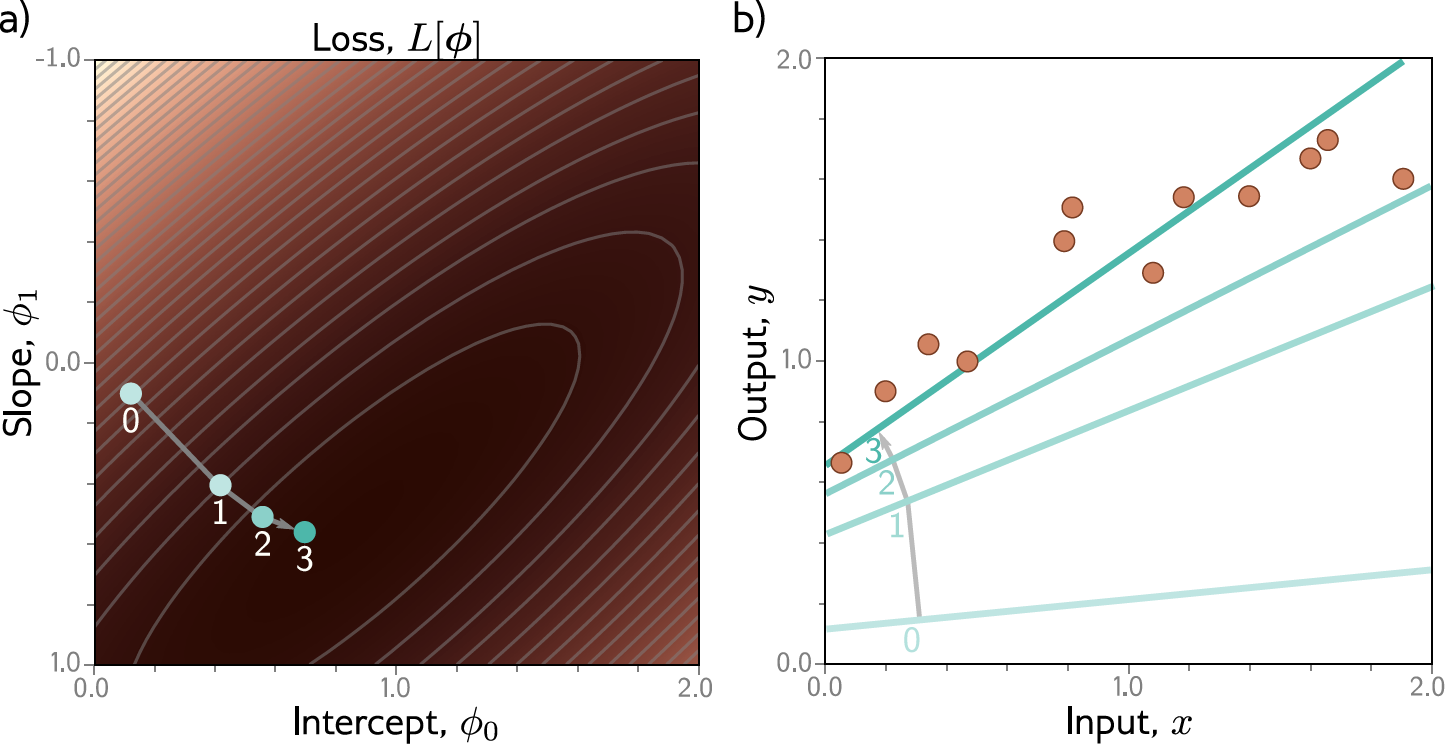
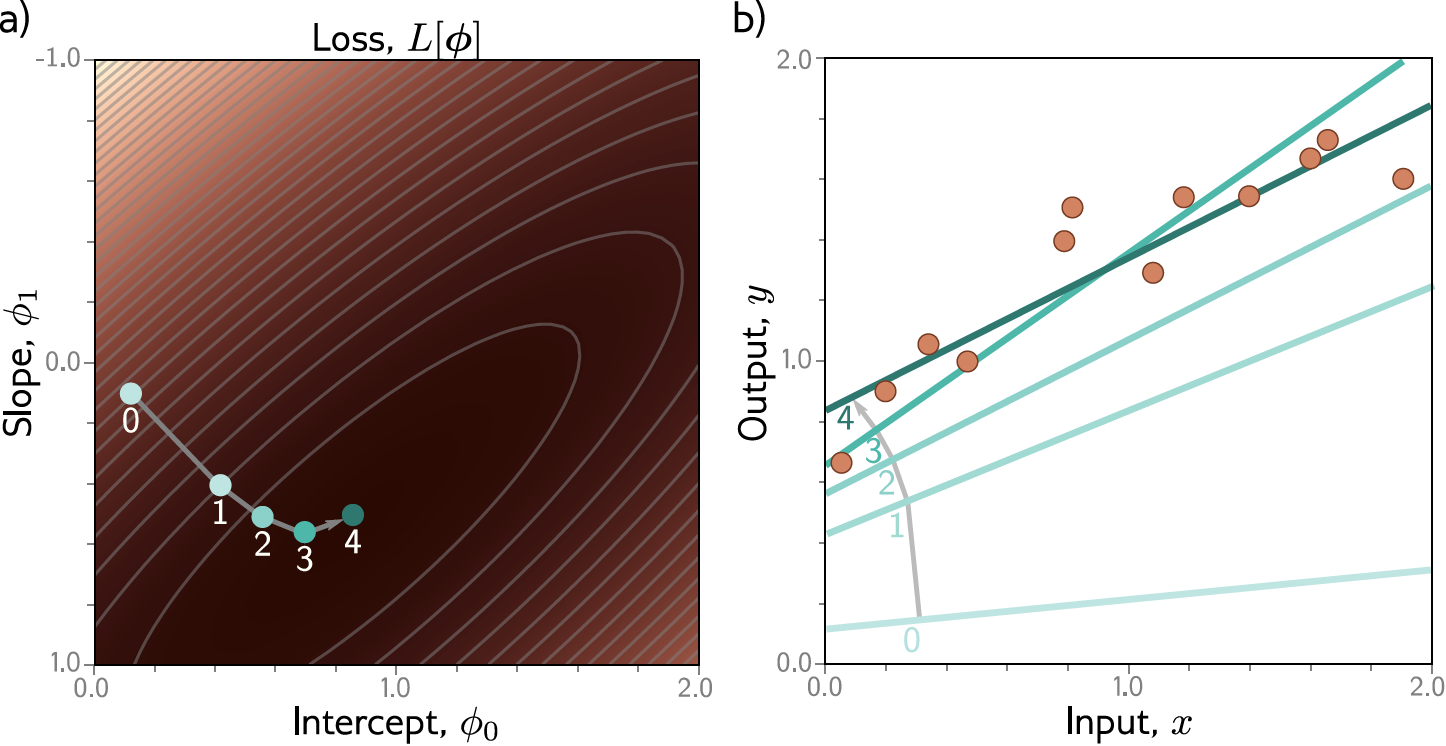
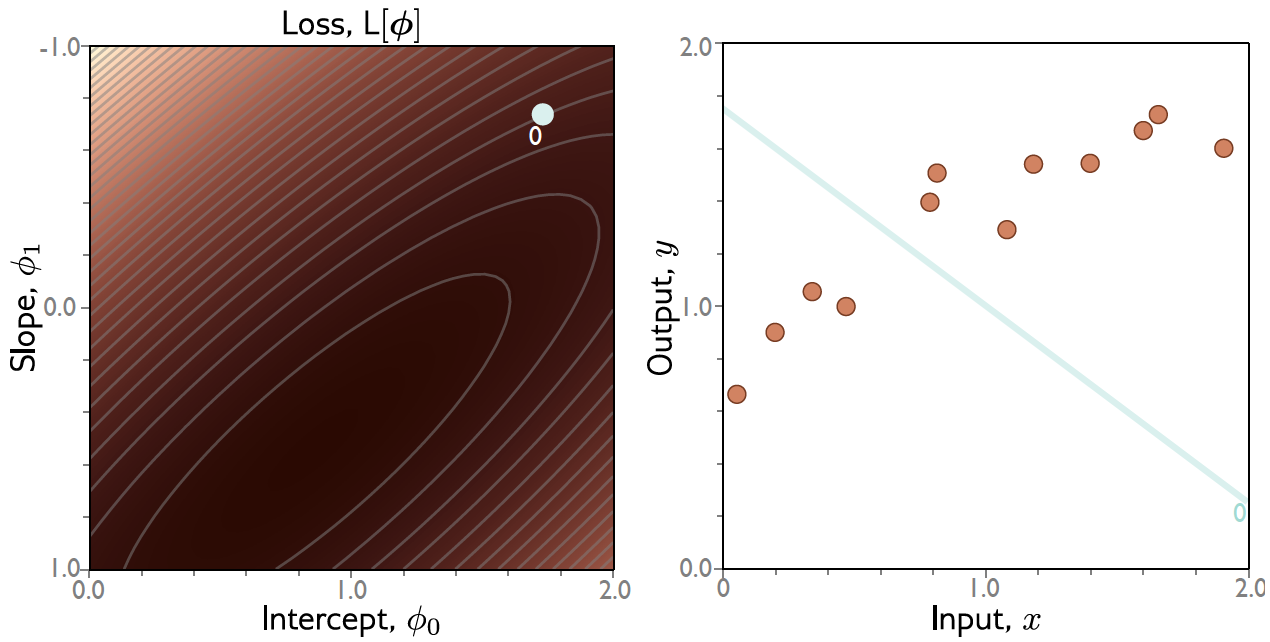
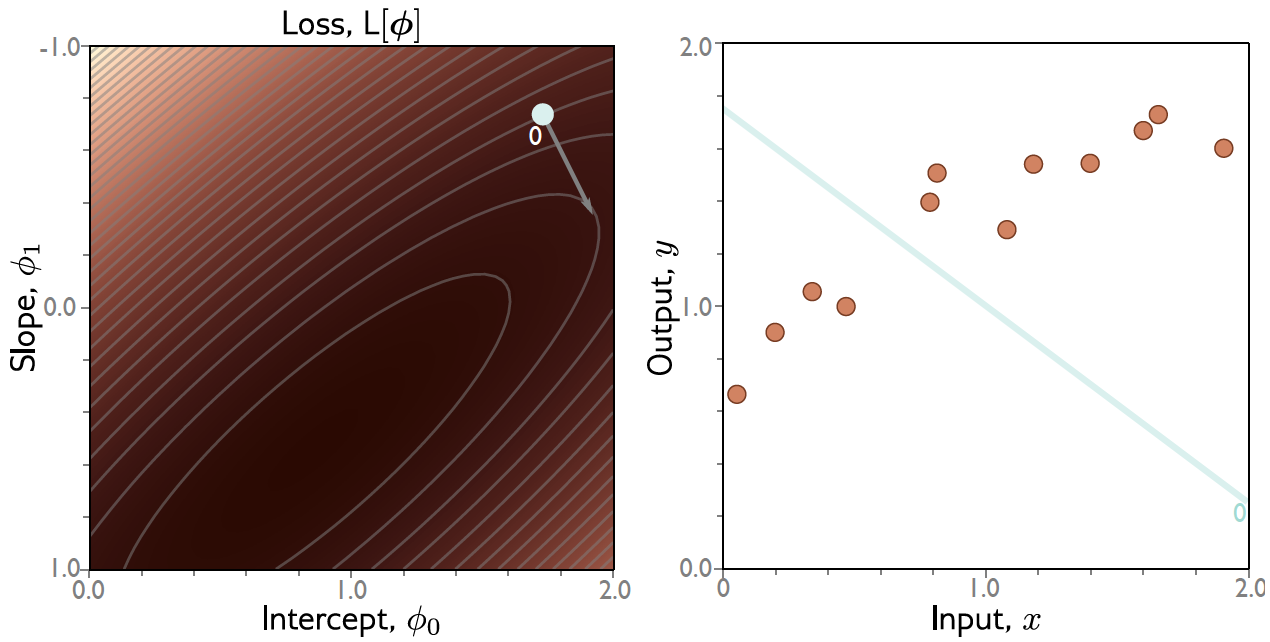
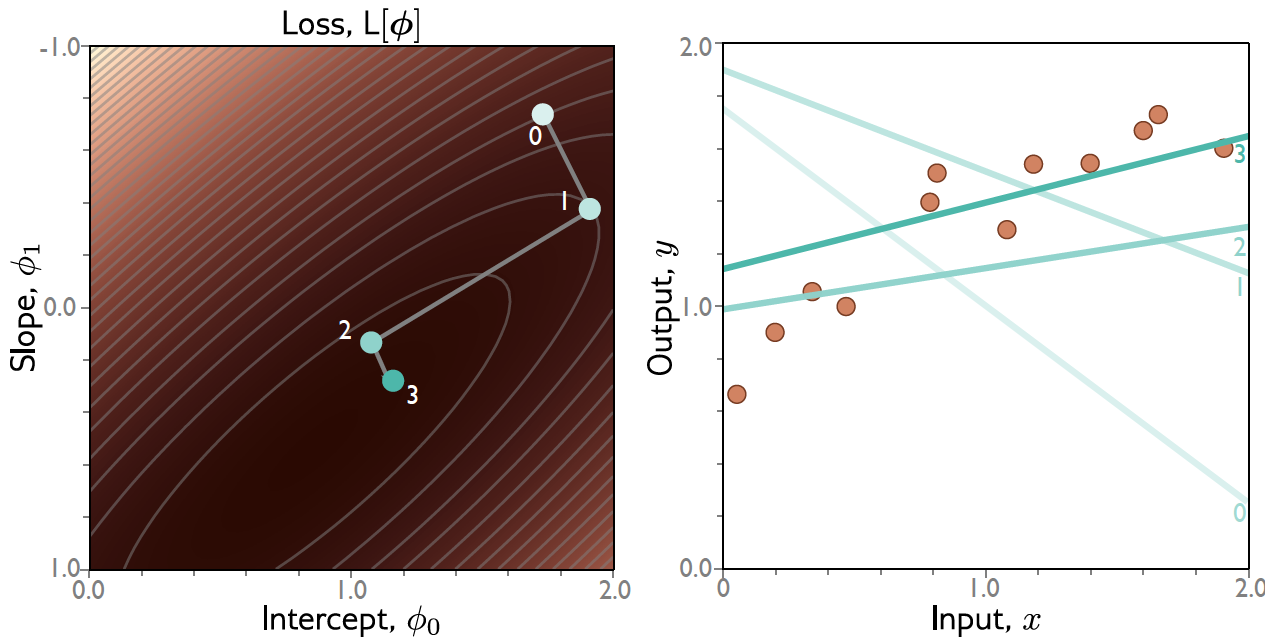
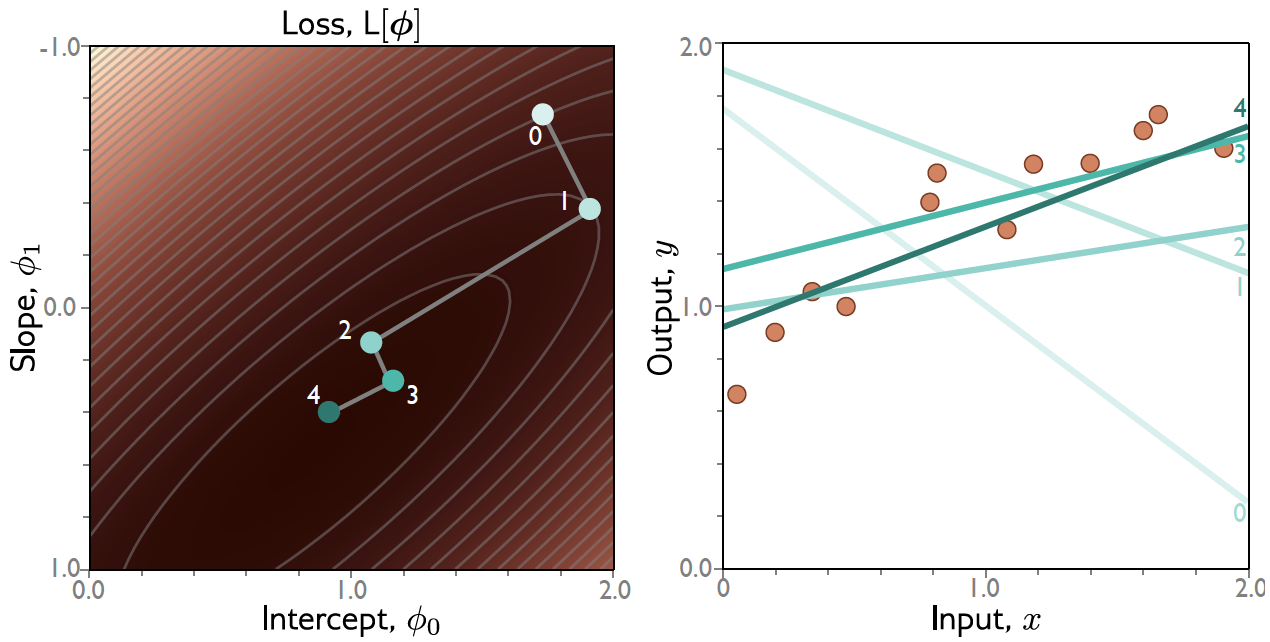
Exemplo: Regressão Linear 1D¶
Exemplo: Regressão Linear 1D¶
Exemplo: Regressão Linear 1D¶
Exemplo: Regressão Linear 1D¶
Exemplo: Regressão Linear 1D¶
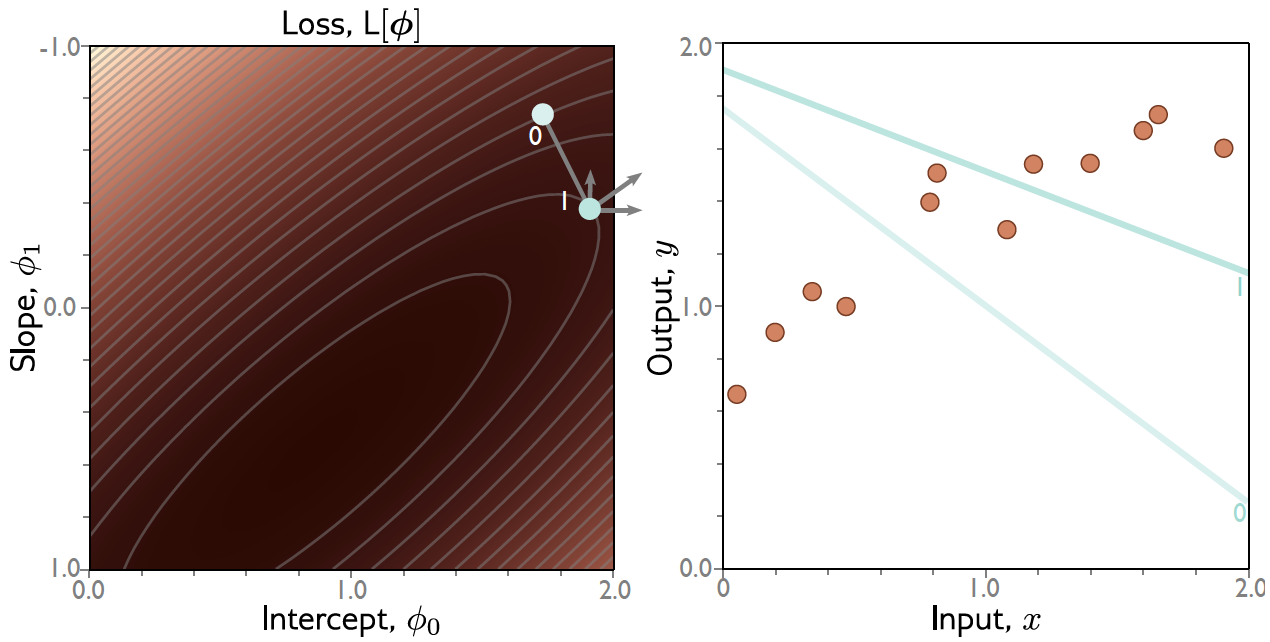
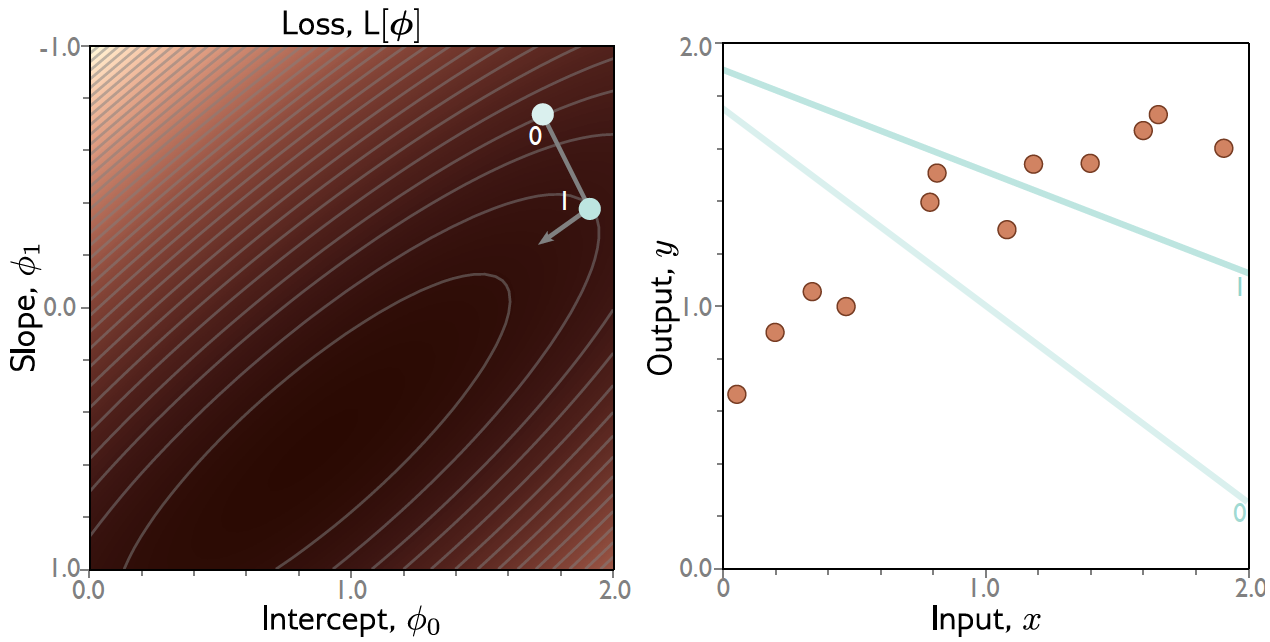
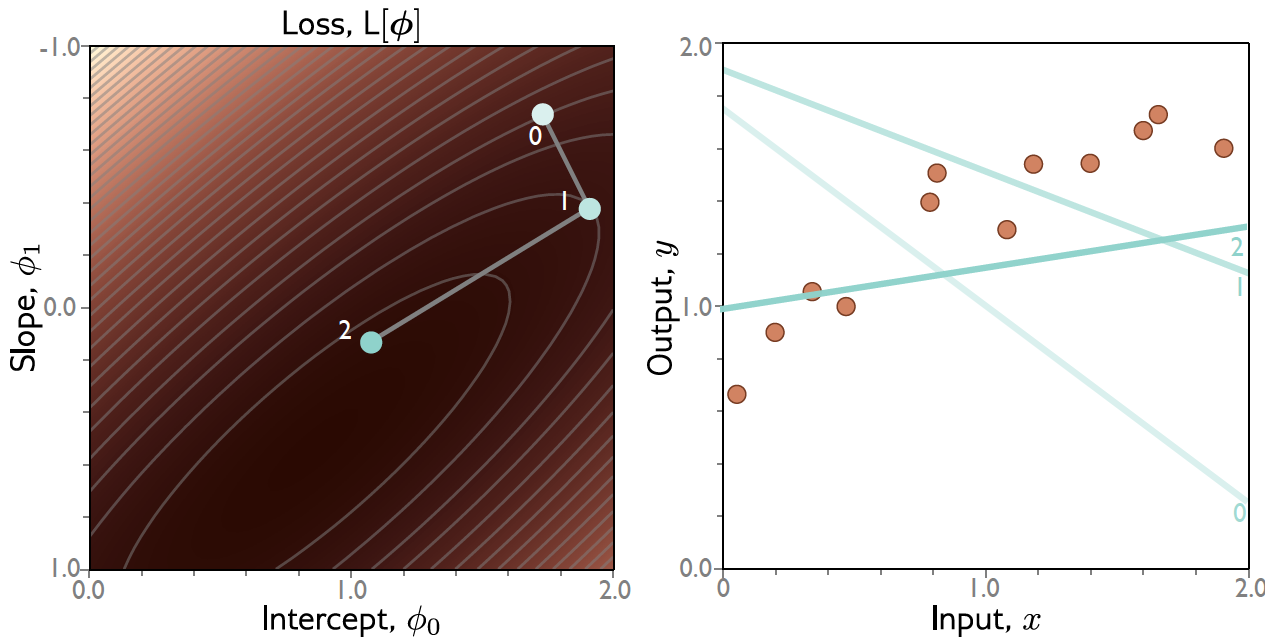
Gradiente Descendente: Exemplo¶
Gradiente Descendente: Exemplo¶
Gradiente Descendente: Exemplo¶
Batch Gradient Descent (BGD)¶
O BGD é a forma mais pura do algoritmo, utilizando o conjunto de treinamento completo ($N$ exemplos) para calcular o gradiente em cada iteração.
- O gradiente calculado é a média de todas as perdas individuais $l_i$: $$ \nabla\mathcal{L} (\mathbf{w}) = \frac{1}{N} \sum_{i=1}^{N} \nabla l_i (\mathbf{w}) $$
- Vantagem: O gradiente é exato (para o conjunto de treinamento), resultando em convergência estável e suave.
- Desvantagem: É computacionalmente caro, pois requer a passagem (forward/backward) por todos os dados em cada passo de atualização.
import numpy as np
# Função simples: para d=2, temos f(w_1,w_2) = w_1*w_1 + w_2*w_2
def f(w):
return np.sum(w*w)
# Gradiente (deriavada) da função
def grad(w):
return 2*w
def gradient_descent(func, grad_func,
w_init, n_epochs=100,
lr=0.001, verbose=0):
i = 0
w = w_init
while i < n_epochs:
# conduct gradient update step
delta_w = -lr * grad_func(w)
w = w + delta_w
if verbose > 0:
print(f"f = {func(w)};\tw: {w}")
i += 1
return w
# Ponto de início
w_init = np.array([10,10])
# Learning rate
lr = 0.01
# Aplica gradient descent
w_opt = gradient_descent(
f, grad, w_init, n_epochs=10,
lr=lr, verbose=1)
f = 192.08000000000004; w: [9.8 9.8] f = 184.47363200000004; w: [9.604 9.604] f = 177.1684761728; w: [9.41192 9.41192] f = 170.15260451635714; w: [9.2236816 9.2236816] f = 163.41456137750941; w: [9.03920797 9.03920797] f = 156.94334474696007; w: [8.85842381 8.85842381] f = 150.72838829498042; w: [8.68125533 8.68125533] f = 144.75954411849915; w: [8.50763023 8.50763023] f = 139.0270661714066; w: [8.33747762 8.33747762] f = 133.5215943510189; w: [8.17072807 8.17072807]
Stochastic Gradient Descent (SGD)¶
O SGD modifica o BGD calculando o gradiente com base em apenas um único exemplo de treinamento ($|\mathcal{S}|=1$).
- O gradiente $\nabla l_i(\mathbf{w})$ é calculado para um exemplo $i$ amostrado aleatoriamente: $$ \mathbf{w}_{t+1} = \mathbf{w}_t - \eta \nabla l_i (\mathbf{w}_t) $$
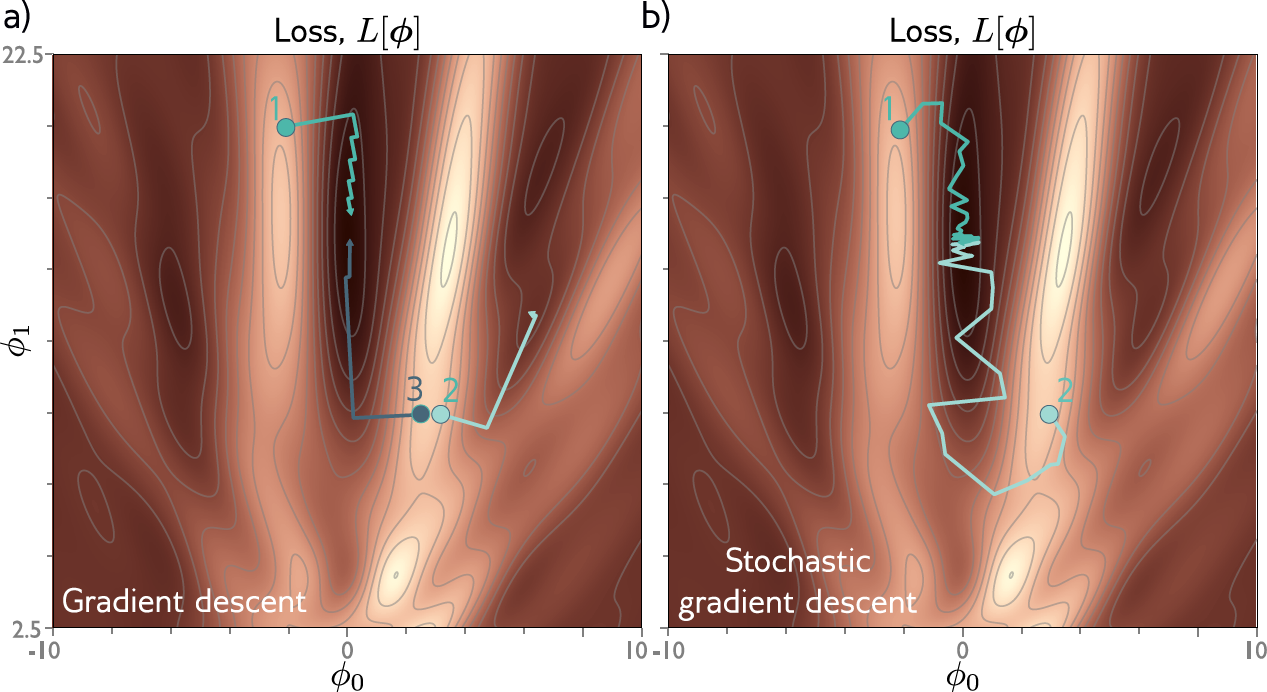
- Vantagem: É muito mais rápido, pois a complexidade por atualização não cresce com $N$. O ruído adicionado pode ajudar a escapar de mínimos locais e pontos de sela.
- Desvantagem: O gradiente é ruidoso (alta variância). A convergência é ruidosa e instável.
Taxa de Aprendizado (Learning Rate): Em SGD, é crucial diminuir $\eta$ ao longo do tempo (schedule), pois o ruído inerente impede a convergência tradicional.
Mini-Batch Gradient Descent (M-BGD)¶
O M-BGD (ou simplesmente SGD) é o padrão moderno, utilizando um subconjunto $\mathcal{B}$ de $M$ exemplos ($1 < M < N$).
- Mini-Batch: Um pequeno grupo de amostras, geralmente com tamanho $M \in$ (potências de 2 são comuns).
- O gradiente é calculado como a média das perdas no mini-batch: $$ \nabla\mathcal{L}_{\mathcal{B}} (\mathbf{w}) = \frac{1}{M} \sum_{i \in \mathcal{B}} \nabla l_i (\mathbf{w}) $$
Benefício do M-BGD: M-BGD equilibra a estabilidade do BGD (estimativa menos ruidosa que SGD puro) com a eficiência do SGD (não precisa processar todos os dados). O paralelismo de hardware (GPUs) é otimizado para o processamento em lotes.
Gradient Descent: Resumo dos Algoritmos¶
| Método | Tamanho do Batch ($M$) | Freq. de Atualização | Custo Computacional |
|---|---|---|---|
| BGD | $N$ (Total de Dados) | Baixa (1/Epoch) | Alto |
| SGD | $1$ | Alta (1/Exemplo) | Baixo |
| M-BGD | $1 < M < N$ | Média (1/Mini-Batch) | Médio |
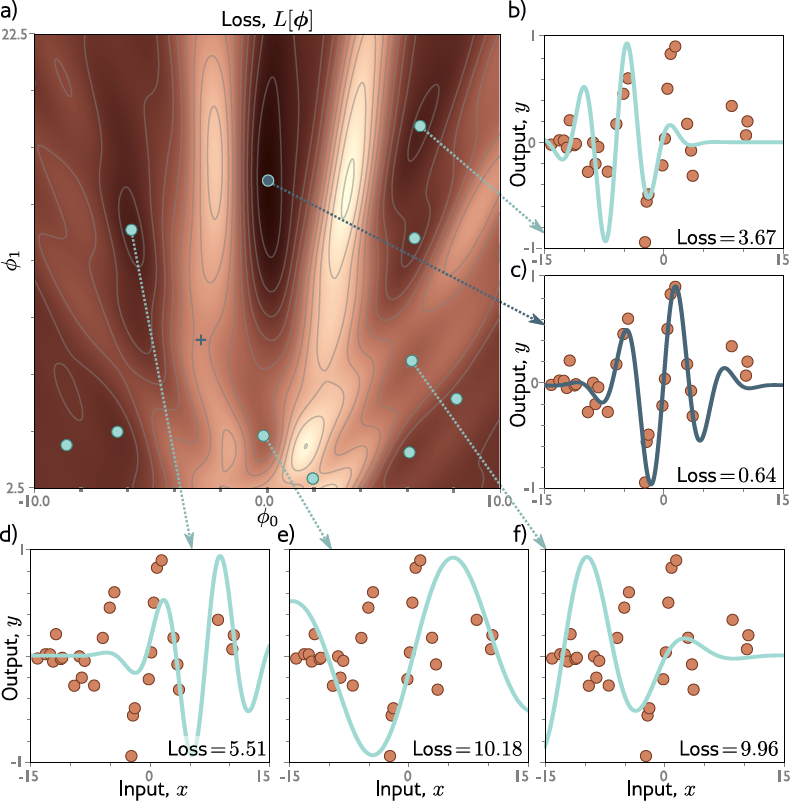
O Desafio dos Gradientes em Redes Neurais¶
Uma rede neural profunda é uma composição massiva de funções (layers ou "gates").
$$ \mathcal{L}(\mathbf{x}; \boldsymbol{\phi}) = \mathcal{L} \circ f^{(L)} \circ \sigma^{(L-1)} \circ \dots \circ \sigma^{(1)} \circ f^{(0)}(\mathbf{x}) $$- O Problema: Precisamos calcular $\nabla\mathcal{L} (\boldsymbol{\phi})$ (o gradiente da perda em relação a cada parâmetro $\mathbf{W}^{(l)}$ e $\mathbf{b}^{(l)}$ em todas as camadas $l$).
- Calcular essas derivadas diretamente é inviável, pois resultaria em expressões extremamente longas e redundantes.
Solução: O algoritmo Back-Propagation (BP). BP utiliza a regra da cadeia para calcular o gradiente de forma eficiente, reutilizando cálculos parciais em uma passagem reversa (backward pass) pela rede.
Leita também: https://xnought.github.io/backprop-explainer/
A Regra da Cadeia (Chain Rule) Revisitada¶
O BP é fundamentado na Regra da Cadeia do cálculo diferencial.
1. Caso Simples (Escalar): Se $z = f(y)$ e $y = g(x)$, a derivada de $z$ em relação a $x$ é o produto das derivadas locais: $$ \frac{dz}{dx} = \frac{dz}{dy} \cdot \frac{dy}{dx} $$
2. Caso Multidimensional (Jacobianos): Se $\mathbf{y} = g(\mathbf{x})$ (mapeamento de $\mathbb{R}^n \to \mathbb{R}^l$) e $\mathbf{z} = f(\mathbf{y})$ (mapeamento de $\mathbb{R}^l \to \mathbb{R}^m$), a derivada é o produto das matrizes Jacobianas (matrizes de derivadas parciais): $$ J_{f \circ g}(\mathbf{x}) = J_f(g(\mathbf{x})) J_g(\mathbf{x}) $$
- Em DL, a perda $\mathcal{L}$ (escalar) depende dos parâmetros $\mathbf{W}$ (matriz), o que torna a notação mais conveniente usando vetores de gradientes.
Backpropagation: O Forward Pass (Ativações)¶
Antes de calcular os gradientes, precisamos executar o Forward Pass (Passagem para Frente). O Forward Pass calcula as ativações de cada camada, que serão usadas posteriormente no Backward Pass para calcular os gradientes.
Notação:
- $\mathbf{x}^{(l)}$: Vetor de ativações da camada $l$.
- $\mathbf{s}^{(l)}$: Vetor de pré-ativações da camada $l$ (somas antes da função $\sigma$).
- $\mathbf{W}^{(l)}, \mathbf{b}^{(l)}$: Parâmetros (pesos e vieses) da camada $l$.
- $\sigma$: Função de ativação (e.g., ReLU, $\text{Tanh}$).
Cálculos Iterativos: $$\mathbf{x}^{(0)} = \mathbf{x} \quad \text{ (Input)}$$ $$\mathbf{s}^{(l)} = \mathbf{W}^{(l)}\mathbf{x}^{(l-1)} + \mathbf{b}^{(l)} \quad (\text{soma ponderada})$$ $$\mathbf{x}^{(l)} = \sigma(\mathbf{s}^{(l)}) \quad (\text{ativação})$$
- Requisito: Todas as pré-ativações $\mathbf{s}^{(l)}$ e ativações $\mathbf{x}^{(l)}$ devem ser armazenadas na memória (trade-off de memória).
Backpropagation: O Backward Pass¶
O Backward Pass calcula os gradientes $\frac{\partial \mathcal{L}}{\partial \mathbf{W}^{(l)}}$ e $\frac{\partial \mathcal{L}}{\partial \mathbf{b}^{(l)}}$ trabalhando de trás para frente (da camada $L$ para a camada 1), utilizando a Regra da Cadeia.
Passo Inicial (Camada de Saída $L$): Gradiente da Perda $\mathcal{L}$
- Cálculo $\frac{\partial \mathcal{L}}{\partial \mathbf{x}^{(L)}}$: Calcule o gradiente da perda $\mathcal{L}$ em relação à saída da rede $\mathbf{x}^{(L)}$ (depende diretamente da função de perda escolhida).
- Cálculo $\frac{\partial \mathcal{L}}{\partial \mathbf{s}^{(L)}}$ (Erro de Saída): Propague este gradiente através da função de ativação $\sigma$ da camada $L$:
- Isto é um produto pontual (elemento a elemento, $\odot$) entre o gradiente da camada seguinte e a derivada local da função de ativação $\sigma'$.
Calculamos os gradientes:
$ \frac{\partial \mathcal{L}}{\partial \mathbf{w}} = -7.68 \quad\quad \frac{\partial \mathcal{L}}{\partial \mathbf{b}} = -3.8 $
Atualizamos os parâmetros (considere a learning rate $\eta = 0.01$):
$w := w - \eta\frac{\partial \mathcal{L}}{\partial \mathbf{w}}= (1) - (0.01) \cdot (-7.68) = 1.0798$
$b := b - \eta\frac{\partial \mathcal{L}}{\partial \mathbf{b}}= (0) - (0.01) \cdot (-3.8) = 0.038$
Com os novos parâmetros, temos um loss menor:
$\mathcal{L}=((1.0798)(2.1)+0.038)−4)^2=2.87$
Backward Pass: Propagação do Erro ($\frac{\partial \mathcal{L}}{\partial \mathbf{x}^{(l-1)}}$)¶
O erro (gradiente da perda) é propagado de volta da pré-ativação $\mathbf{s}^{(l)}$ para a ativação da camada anterior $\mathbf{x}^{(l-1)}$.
- Isto é realizado através da multiplicação pelo transposto ($\mathbf{W}^{(l)T}$) da matriz de pesos $\mathbf{W}^{(l)}$.
- Este cálculo informa como uma mudança na camada anterior $\mathbf{x}^{(l-1)}$ afeta a perda $\mathcal{L}$ através das conexões em $\mathbf{W}^{(l)}$.
Fórmula de Propagação (Gradients w.r.t. Activations): $$ \frac{\partial \mathcal{L}}{\partial \mathbf{x}^{(l-1)}} = \left(\mathbf{W}^{(l)}\right)^T \frac{\partial \mathcal{L}}{\partial \mathbf{s}^{(l)}} $$
Continuação: Após calcular $\frac{\partial \mathcal{L}}{\partial \mathbf{x}^{(l-1)}}$, a Regra da Cadeia é aplicada novamente para obter $\frac{\partial \mathcal{L}}{\partial \mathbf{s}^{(l-1)}}$ e assim sucessivamente.
Backward Pass: Gradientes dos Parâmetros¶
Uma vez que o vetor de erro $\frac{\partial \mathcal{L}}{\partial \mathbf{s}^{(l)}}$ (o "erro" da camada $l$) é conhecido, o cálculo dos gradientes dos parâmetros $\mathbf{W}^{(l)}$ e $\mathbf{b}^{(l)}$ é direto e local.
1. Gradiente dos Pesos ($\mathbf{W}^{(l)}$): A derivada da perda em relação ao peso $\mathbf{W}^{(l)}_{i,j}$ é o produto do erro $\frac{\partial \mathcal{L}}{\partial \mathbf{s}^{(l)}_i}$ pela ativação da camada anterior $\mathbf{x}^{(l-1)}_j$. $$ \frac{\partial \mathcal{L}}{\partial \mathbf{W}^{(l)}} = \frac{\partial \mathcal{L}}{\partial \mathbf{s}^{(l)}} \left(\mathbf{x}^{(l-1)}\right)^T $$
2. Gradiente dos Vieses ($\mathbf{b}^{(l)}$): O gradiente do viés é simplesmente o erro da camada: $$ \frac{\partial \mathcal{L}}{\partial \mathbf{b}^{(l)}} = \frac{\partial \mathcal{L}}{\partial \mathbf{s}^{(l)}} $$
Frameworks Modernos: Diferenciação Algorítmica¶
Felizmente, não precisamos implementar o Backward Pass manualmente em cada projeto.
- Frameworks de Deep Learning (PyTorch, TensorFlow) utilizam Diferenciação Algorítmica (Algorithmic Differentiation) para calcular gradientes automaticamente.
- Cada componente (função linear, ReLU, perda) sabe como calcular suas próprias derivadas locais.
- O framework constrói o grafo computacional e usa a regra da cadeia para compilar o Backward Pass, garantindo eficiência máxima (muitas vezes duas vezes mais caro que o Forward Pass).
import torch.optim as optim
# Definição do modelo e perda (omissos)
# model = ...
# loss = ...
# 1. Zera gradientes (evita acumulação)
optimizer.zero_grad()
# 2. Forward Pass
predictions = model(inputs)
loss_value = criterion(predictions, targets)
# 3. Backward Pass (Cálculo Automático)
loss_value.backward() # Computa dL/dW para todos os W
# 4. Atualização (Gradient Descent)
optimizer.step() # w ← w - η * dL/dw
import torch
import torch.nn as nn
torch.manual_seed(1)
w = torch.empty(2, 3)
nn.init.xavier_normal_(w)
print(w)
tensor([[ 0.4183, 0.1688, 0.0390],
[ 0.3930, -0.2858, -0.1051]])
w = torch.tensor(1.0, requires_grad=True)
b = torch.tensor(0.5, requires_grad=True)
x = torch.tensor([1.4])
y = torch.tensor([2.1])
z = torch.add(torch.mul(w, x), b)
loss = (y-z).pow(2).sum() # Erro Quadrático
loss.backward()
print('dL/dw : ', w.grad)
print('dL/db : ', b.grad)
print(2 * x * ((w * x + b) - y)) # Computando dL/dw
dL/dw : tensor(-0.5600) dL/db : tensor(-0.4000) tensor([-0.5600], grad_fn=<MulBackward0>)
Otimizadores¶
|
Otimizador mais utilizado é o Adam (Adaptive moment estimation): $$ m_t = \beta_1 m_{t-1} + (1-\beta_1)\nabla_\theta\mathcal{L} $$$$ v_t = \beta_2 v_{t-1} + (1-\beta_2)(\nabla_\theta\mathcal{L})^2 $$$$ \hat{m}_t = \frac{m_t}{1-\beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1-\beta_2^t} $$$$ \theta_{t+1} = \theta_t - \eta \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon} $$ |
Landscape da função de loss¶
Otimização por Gradiente Descendente¶
Resumo¶
|
 Leitura Recomendada: Capítulo 8.
Leitura Recomendada: Capítulo 8.
|
Perguntas e Discussão¶
- O Mini-Batch Gradient Descent (M-BGD) é o padrão atual. Discuta as razões pelas quais o M-BGD (e não o Batch Gradient Descent puro) se tornou o método preferido, considerando a eficiência computacional em arquiteturas modernas (GPUs) e as propriedades de convergência.
- Funções de custo em Deep Learning são tipicamente não-convexas. A literatura sugere que, para redes profundas e largas, mínimos locais com alto custo são raros. Contudo, o M-BGD introduz ruído que pode ajudar a escapar de mínimos locais. Como a natureza ruidosa do SGD se manifesta na trajetória de otimização e por que isso é crucial para evitar pontos de sela (saddle points) em espaços de alta dimensão?
- Backpropagation (BP) é essencial porque evita o cálculo redundante de gradientes via regra da cadeia. O que exatamente precisa ser armazenado durante o Forward Pass para que o Backward Pass funcione?
- O otimizador Adam (Adaptive moment estimation) combina ideias do Momentum e do AdaGrad. Explique o papel da normalização (escalonamento pelo quadrado da média dos gradientes) no Adam e como isso ajuda a equilibrar as taxas de atualização entre diferentes camadas ou parâmetros do modelo.