Visão Computacional

Processamento de Imagens Coloridas

Prof. Dr. Denis Mayr Lima Martins

Pontifícia Universidade Católica de Campinas

Objetivos de Aprendizagem

---

• Compreender os diferentes modelos de cores.
• Explicar como o espaço RGB descreve cada pixel por meio dos componentes R, G e B, incluindo suas limitações em relação à percepção humana.
• Realizar operações lineares e não‑lineares sobre canais/componentes individuais.
• Desenvolver habilidades práticas com ferramentas como OpenCV ou scikit‑image para converter espaços de cor.

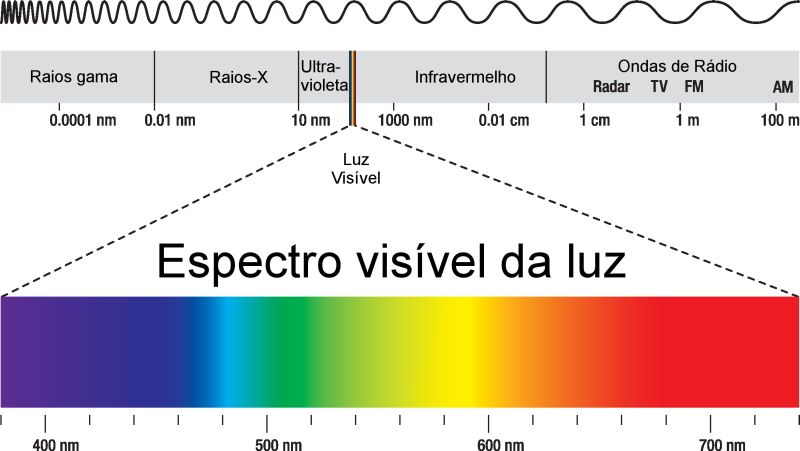
Fundamento de Cores

---

• Cor: percepção visual resultante da interação entre luz, objeto e observador.
• Modelo físico: a luz é uma onda eletromagnética.
• Faixa visível: 400 nm (violeta) – 700 nm (vermelho).

Espectro Eletromagnético. Fonte: DataHackers.rs.

Imagem Colorida

---

Canal / Banda: Subconjunto da imagem que contém intensidades de um componente específico do espaço colorido. Uma imagem colorida é representada por três componentes de intensidade em cada pixel: $f(x,y) = [R(x,y), G(x,y), B(x,y)]$

Canais RGB. Fonte: Geeks for Geeks.

Modelos de Cor

---

Espaço Colorido: Modelo matemático que descreve como combinações de componentes formam todas as cores perceptíveis (ex.: RGB, HSV, CIELAB). RGB (Red, Green, Blue): aditivo, usado em telas. CMY/CMYK (Cyan, Magenta, Yellow, Black): subtrativo, usado em impressão. HSI (Hue, Saturation, Intensity): alinhado à percepção humana.

Canais RGB. Fonte: Color Meanings.

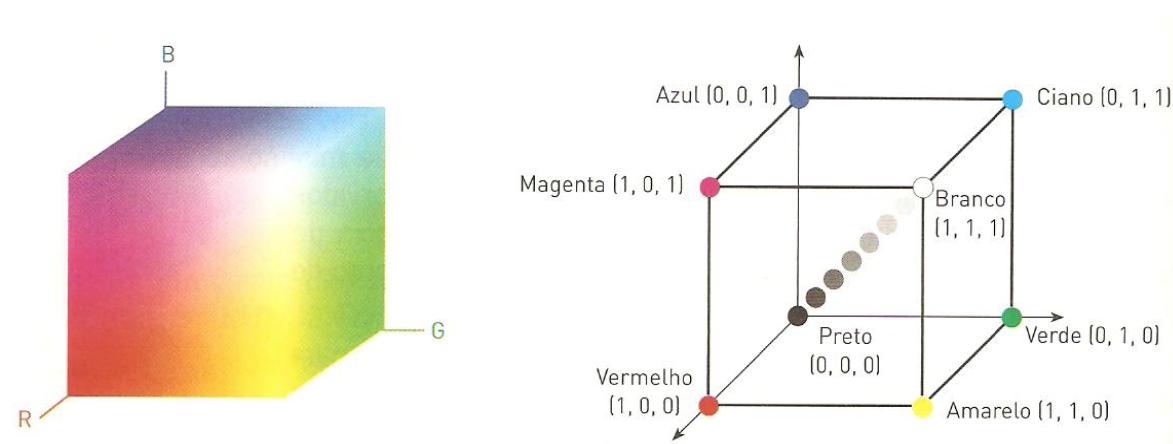
Modelos de Cor: RGB

---

• Cada pixel é descrito por três componentes de intensidade: $R$, $G$ e $B$.
• Os valores são normalmente discretizados em $b_R,b_G,b_B$ bits, resultando num intervalo $[0,2^{b}-1]$.
• Representação Geométrica: O conjunto de todas as combinações possíveis forma um cubo tridimensional no espaço $(R,G,B)$.

Cubo do Modelo RGB. Fonte: Tudo sobre a cor.

Modelos de Cor: RGB (cont.)

---

Cada vértice do cubo corresponde a uma das oito cores extremas:

• Linearidade: Combinações lineares de cores (ex.: mistura de vermelho e verde) são pontos ao longo das arestas.
• Percepção luminosa: A distância euclidiana entre dois pontos não reflete necessariamente a diferença perceptual.
• A luminância $L = 0,2126R+0,7152G+0,0722B$ (para sRGB) descreve melhor o brilho percebido.

Cubo do Modelo RGB. Fonte: Wikipedia.

Modelos de Cor: HSV

---

• Cada pixel é descrito por três componentes:
  • $H \in [0^\circ,360^\circ)$ (matiz)
  • $S \in [0,1]$ (saturação)
  • $V \in [0,1]$ (valor / luminância)
• Representação Geométrica: O conjunto de todas as combinações forma um cilindro no espaço tridimensional $(H,S,V)$. A base circular corresponde a $V=1$ (nível máximo de luminância); cada raio da base representa um matiz com saturação máxima; a altura do cilindro é dada por $V$.

Cilindro do Modelo HSV. Fonte: Wikipedia.

Modelos de Cor: HSV (cont.)

---

• O modelo é projetado para refletir a percepção humana de cor:
  • Matiz determina a cor propriamente dita (vermelho, verde, azul…);
  • Saturação indica quão "pura" essa cor está;
  • Valor controla o brilho.
• Pontos na borda do cilindro ($S=1$) correspondem a cores "puras" (sem mistura de branco).
• À medida que $V$ diminui, os pontos se movem em direção ao centro do cilindro, representando tons mais escuros ou cinzentos.
• Alterações apenas no componente $H$ giram o ponto ao redor da base circular, mudando a cor sem alterar saturação nem brilho.

RGB (esquerda) e HSV (direita). Fonte: ResearchGate.

Usando Scikit-Image

---

from skimage import data
from skimage.color import rgb2gray,rgb2hsv

original = data.astronaut()
grayscale = rgb2gray(original)
show_images(original, grayscale)

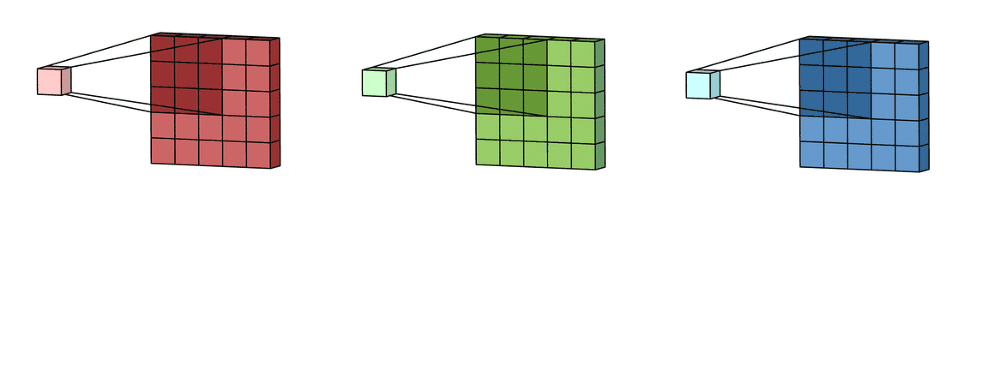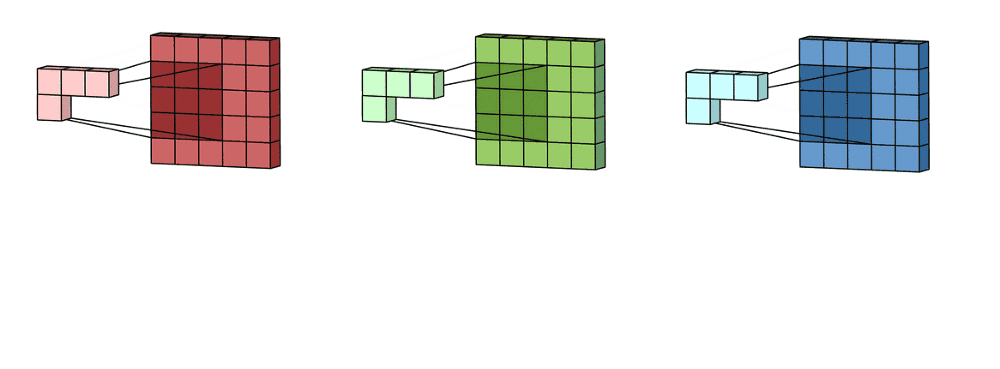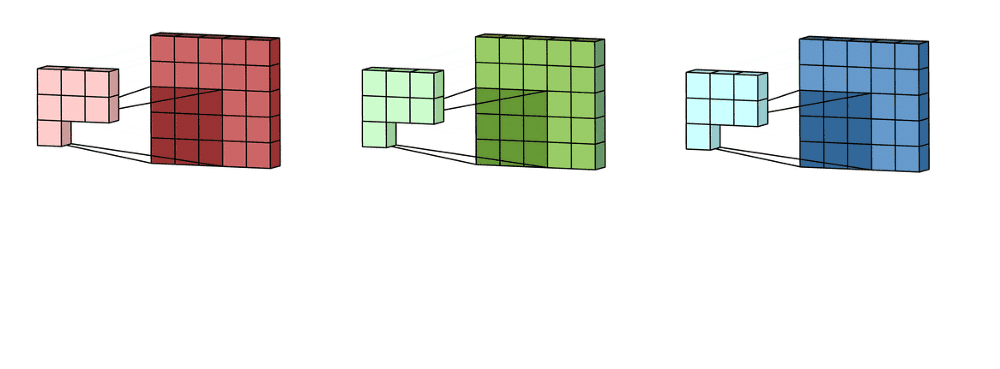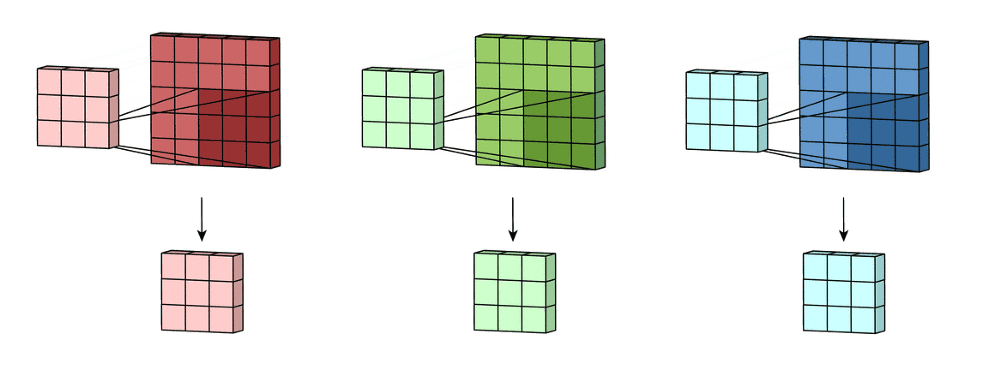
Observando canais

---

figure, axarr = plt.subplots(1,3, figsize=(10,10))
axarr[0].imshow(original[:,:,0], cmap= 'Reds')
axarr[1].imshow(original[:,:,1], cmap= 'Greens')
axarr[2].imshow(original[:,:,2], cmap= 'Blues')
for ax in axarr.ravel():
        ax.set_axis_off()
plt.show()

Histograma dos Canais RGB

---

plt.figure(figsize=(4, 2))
color = ('b','g','r')
for i,col in enumerate(color):
    histr = cv2.calcHist([original],[i],None,[256],[0,256])
    plt.plot(histr,color = col)
    plt.xlim([0,256])
plt.title('Histograma')
plt.xlabel('Intensidade de pixel')
plt.ylabel('Quantidade')
plt.show()

Modelo HSV: Aplicação

---

• Em geral, os objetos presentes em uma cena digital exibem tonalidades (tons) e níveis de luminosidade distintos. No espaço de cores RGB, tanto o tom quanto a luminosidade são obtidos como combinações lineares dos três canais primários R, G e B.
• Ao converter para o modelo HSV (Hue–Saturation–Value), esses atributos se tornam atributos independentes: o canal H representa exclusivamente o tom, enquanto o canal V encapsula a luminosidade.
• Aplicando um limiar ao canal H (ou ao canal V, conforme a aplicação), podemos separar uma região de interesse.

# Carrega a imagem de exemplo (café)
rgb_img = data.coffee()
# Converte a representação RGB para HSV.
hsv_img = rgb2hsv(rgb_img)
# Canal de tom (primeiro eixo na matriz HSV)
hue_img = hsv_img[:, :, 0]
# Canal de luminosidade (terceiro eixo)
value_img = hsv_img[:, :, 2] 

Modelo HSV: Aplicação (cont.)

---

fig, (ax0, ax1, ax2) = plt.subplots(ncols=3, figsize=(8, 3))
ax0.imshow(rgb_img)
ax0.set_title("Imagem RGB")
ax0.axis('off') 
# cmap 'hsv' permite observar o ciclo angular das tonalidades
ax1.imshow(hue_img, cmap='hsv') 
ax1.set_title("Canal Hue (matiz)")
ax1.axis('off')
# Exibe o canal Value (luminosidade)
ax2.imshow(value_img)
ax2.set_title("Canal Value (luminosidade)")
ax2.axis('off')
plt.tight_layout()

Modelo HSV: Aplicação (cont.)

---

Separa e visualiza os componentes de cor mais relevantes para tarefas de segmentação baseada em tom ou luminosidade.

# Definição do limiar de tom (hue)
hue_threshold = 0.04
# Criação de uma imagem binária
binary_img = hue_img > hue_threshold 

Modelo HSV: Aplicação (cont.)

---

Separa e visualiza os componentes de cor mais relevantes para tarefas de segmentação baseada em tom ou luminosidade.

fig, (ax0, ax1) = plt.subplots(ncols=2, figsize=(10, 2))
# `hue_img.ravel()` converte a matriz 2D em um vetor 1D
ax0.hist(hue_img.ravel(), bins=512)
ax0.set_title("Histograma do canal Hue (threshold em vermelho)")
# Linha vermelha pontilhada indica o ponto do limiar
ax0.axvline(x=hue_threshold, color='r', linestyle='dashed', linewidth=2) 
# Evita que valores fora de interesse distorçam a escala
ax0.set_xbound(0, 0.12)
ax1.imshow(binary_img)
ax1.set_title("Imagem Binarizada (Hue-thresholded)")
ax1.axis('off')
fig.tight_layout()

Modelo HSV: Removendo parcialmente a sombra

---

fig, ax0 = plt.subplots(figsize=(3, 3))
value_threshold = 0.10
# Construção da máscara binária que combina duas condições:
# hue_img > hue_threshold: pixels cujo tom excede o limite.
# value_img < value_threshold: pixels com brilho inferior ao limiar.
# Considera cor dominante e contraste de luminosidade
binary_img = (hue_img > hue_threshold) | (value_img < value_threshold) 
ax0.imshow(binary_img)
ax0.set_title("Imagem binarizada\n com limiar em Hue e Value")
ax0.axis('off')
plt.show()

Alinhamento de Histogramas (Histogram Matching)

---

• Objetivo: Transformar a distribuição de intensidades (histograma) de uma imagem‑fonte para coincidir com a de uma imagem‑referência.
• Se as imagens possuírem múltiplos canais, o alinhamento é feito independentemente para cada canal, contanto que o número de canais seja igual em ambas.
• Resultado: A imagem ajustada mantém a mesma estrutura espacial (textura, bordas) mas com tonalidade e contraste semelhantes ao alvo.

Exemplo de Alinhamento de Histograma. Fonte: OIL MCUT - Digital Image Processing.

Alinhamento de Histogramas: Aplicação

---

Procedimento:

1. Calcula o histograma acumulativo (CDF) da fonte e da referência.
2. Para cada nível de intensidade na fonte, encontra o valor correspondente que possui o mesmo CDF na referência.
3. Substitui os pixels da fonte pelos valores mapeados, preservando a ordem dos intensidades.

from skimage import exposure
from skimage.exposure import match_histograms

reference = data.coffee()  
image     = data.chelsea()
# Alinhamento de histogramas: cada canal RGB é tratado separadamente
matched = match_histograms(image, reference, channel_axis=-1)

Alinhamento de Histogramas: Aplicação (cont.)

---

Pode ser usado como normalização leve em processamento de imagens, especialmente quando as imagens foram capturadas de fontes diferentes ou sob condições distintas (ex.: iluminação).

fig, (ax1, ax2, ax3) = plt.subplots(nrows=1, ncols=3, figsize=(8, 3))
for ax in (ax1, ax2, ax3):
    ax.set_axis_off()
ax1.imshow(image)
ax1.set_title('Fonte')
ax2.imshow(reference)
ax2.set_title('Referência')
ax3.imshow(matched)
ax3.set_title('Ajustado')
plt.tight_layout()

Tinting imagens em Grayscale (cont.)

---

• Já vimos que manipulação de cores pode ser útil em tarefas de realce de regiões de interesse.
• Podemos manipular cores artificialmente uma imagem em grayscale para destacar alguma região. Um processo conhecido como tinting.
• A maneira mais simples de obter uma imagem tintada é definir cada canal RGB como a imagem em escala de cinza multiplicada por um fator diferente para cada canal.

from skimage import color
from skimage import img_as_float

# Carrega a imagem de câmera do exemplo (reduzida em 2× para acelerar)
grayscale_image = img_as_float(data.camera()[::2, ::2])
# Converte para RGB (três canais iguais)
image = color.gray2rgb(grayscale_image)
# Fatores de multiplicação para os canais R, G e B
red_multiplier   = [1, 0, 0]   # apenas vermelho
yellow_multiplier = [1, 1, 0]  # vermelho + verde → amarelo

Tinting imagens em Grayscale (cont.)

---

fig, (ax0, ax1, ax2) = plt.subplots(ncols=3, figsize=(8, 4))
ax0.imshow(grayscale_image, cmap="gray")
ax0.set_axis_off()
ax1.imshow(red_multiplier * image)
ax1.set_axis_off()
ax2.imshow(yellow_multiplier * image)
ax2.set_axis_off()
plt.show()

Tinting imagens em Grayscale: Modelo HSV

---

• Em muitos casos, lidar com valores RGB pode não ser ideal.
• Vamos usar o modelo HSV para tintar a imagem.

def colorize(image, hue, saturation=1):
    """Adiciona a cor da matiz fornecida a uma imagem RGB.

    Por padrão, define a saturação como 1 para que as cores “explodam”.
    """
    hsv = color.rgb2hsv(image) # Converte a imagem RGB para HSV
    hsv[:, :, 1] = saturation # Define a matiz e saturação desejadas
    hsv[:, :, 0] = hue
    return color.hsv2rgb(hsv) # Converte de volta para RGB

Tinting imagens em Grayscale: Modelo HSV (cont.)

---

hue_rotations = np.linspace(0, 1, 6)
fig, axes = plt.subplots(nrows=1, ncols=6, figsize=(10, 5))

for ax, hue in zip(axes.flat, hue_rotations):
    # Reduzimos a saturação para dar um visual “vintage”.
    tinted_image = colorize(image, hue, saturation=0.3)
    ax.imshow(tinted_image, vmin=0, vmax=1)
    ax.set_axis_off()
fig.tight_layout()

Convolução de Imagens Coloridas

Convolução de Imagens Coloridas

---

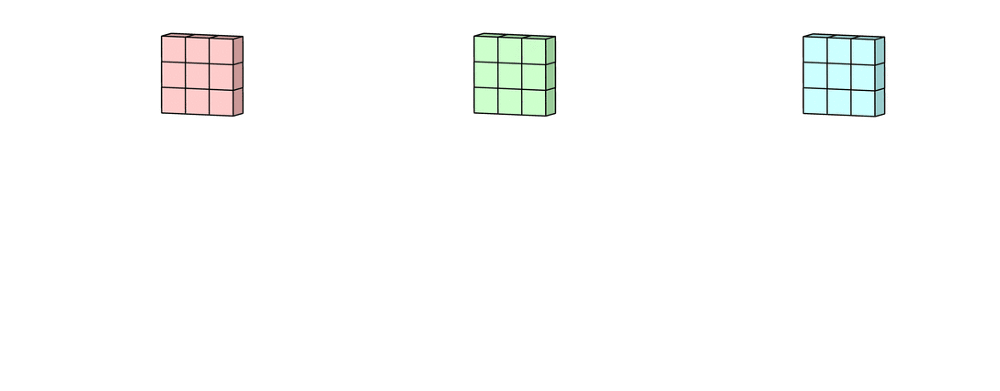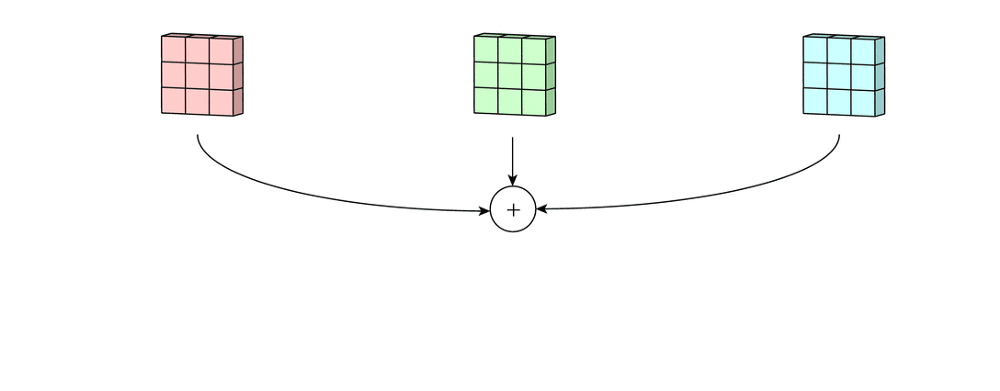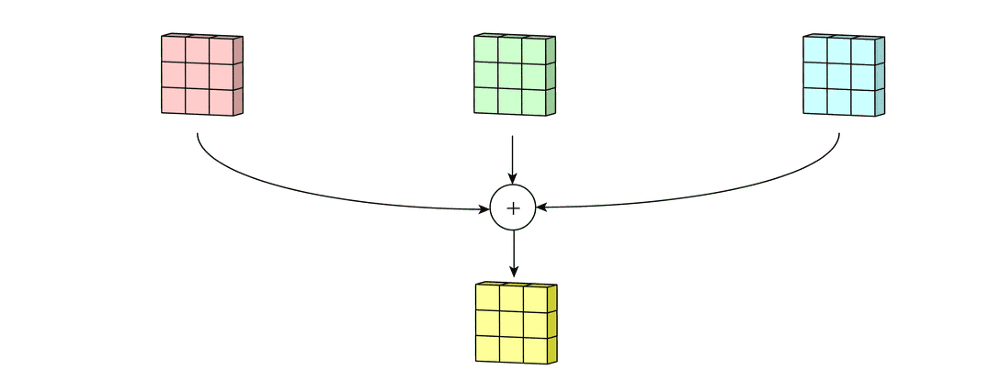
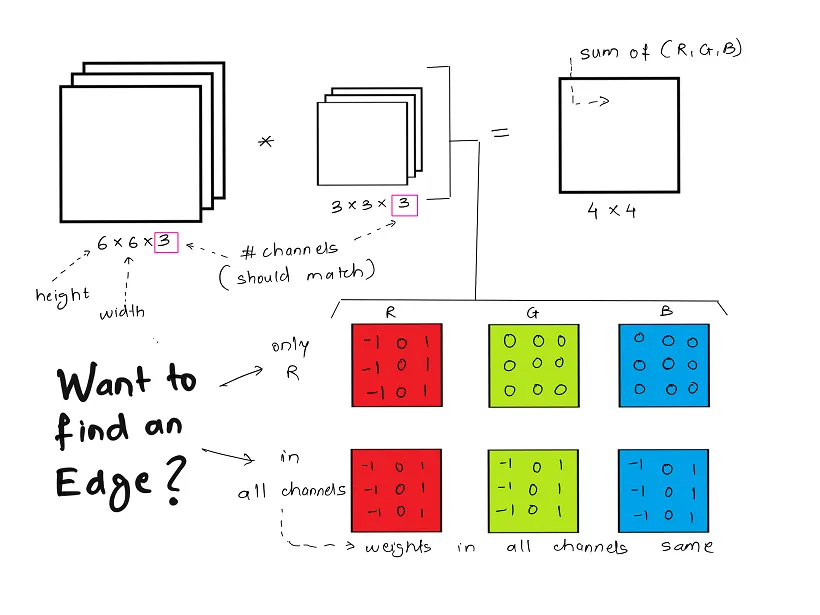
• A convolução é aplicada de forma independente em cada canal:
  • $(I * K)_c(x,y) = \sum_{m}\sum_{n} I_c(x-m,\;y-n)\,K(m,n)$, onde $c \in \{R,G,B\}$.

Convolução em Imagem RGB. Fonte: Amaarora.

• Implementação em Excel por Thom Lane: link para o Google Sheets.

Convolução de Imagens Coloridas (cont.)

---

Na terminologia de Visão Computacional, um feature map é gerado por canal e, então, somado para formar o resultado final da operação de convolução.

Resultado da Convolução em Imagem RGB. Fonte: Amaarora.

Convolução de Imagem Colorida (cont.)

---

Explore o CNN Explainer: https://poloclub.github.io/cnn-explainer/

Convolução em Imagem RGB. Fonte: DataHackers.rs.

Convolução de Imagem Colorida (cont.)

---

Convolução em Imagem RGB. Fonte: DataHackers.rs.

Convolução de Imagem Colorida: Exemplo

---

original = data.astronaut()
kernel = np.ones((5,5), np.float32) / 25 # Filtro de média 
media_img = cv2.filter2D(original, -1, kernel) # Convolução
figure, axarr = plt.subplots(1,2, figsize=(6,6))
axarr[0].imshow(original, cmap= 'gray')
axarr[0].set_title("Imagem Original")
axarr[1].imshow(media_img, cmap= 'gray')
axarr[1].set_title("Imagem Suavizada")
for ax in axarr.ravel(): ax.set_axis_off()
plt.show()

Resumo

---

Fundamentos de Cores: Espaços coloridos, canais, percepções visuais. Representação RGB: Cada pixel possui três componentes lineares $(R,G,B)$. Convolução: Operações separadas por canal. O resultado final combina as respostas dos três canais em uma imagem RGB coerente. Base para as Redes Neurais Convolucionais. Leitura adicional: CNN Explainer: Learning Convolutional Neural Networks with Interactive Visualization, por Wang, Zijie J., Robert Turko, Omar Shaikh, Haekyu Park, Nilaksh Das, Fred Hohman, Minsuk Kahng, and Duen Horng Chau. IEEE Transactions on Visualization and Computer Graphics (TVCG), 2020.

Leitura Recomendada: Capítulo 6.