Visão Computacional¶
Redes Neurais para Classificação de imagens¶
Prof. Dr. Denis Mayr Lima Martins¶
Pontifícia Universidade Católica de Campinas¶
Objetivos de Aprendizagem¶
- Compreender a estrutura e funcionamento do perceptron clássico, incluindo sua relação com a função logística.
- Analisar o Multi‑Layer Perceptron (MLP) como extensão do perceptron, destacando camadas ocultas, funções de ativação não‑lineares e topologia geral.
- Descrever o algoritmo de treinamento baseado em back‑propagation e a otimização de pesos via gradiente descendente.
- Compreender estratégias de validação cruzada (k‑fold) para avaliação robusta de modelos.
- Discutir os conceitos de viés e variância, suas implicações na generalização e estratégias de mitigação.
- Entender métodos de regularização (L1/L2, dropout) e suas aplicações práticas em redes neurais.
Neurônio Artificial¶
Warren McCulloch e Walter Pitts. Criadores do primeiro modelo de neurônio artificial (1943). Fonte: History of Information.
|
Neurônio Artificial. Fonte: Tahseen Mulla.
|
Perceptron¶
|
Visão Geral do Perceptron. Image Source: Sebastian Raschka.
|
Perceptron Learning Rule¶
- Dado um exemplo $(\mathbf{x},y)$, onde $y\in\{0,1\}$ é o rótulo verdadeiro, calcula‑se a predição $\hat{y}=f(z)$.
- Se a predição estiver incorreta ($e=y-\hat{y}\neq 0$), os pesos e viés são ajustados na direção que reduz o erro.
- $\mathbf{w}\leftarrow\mathbf{w}+\eta\,e\,\mathbf{x}$ e $b\leftarrow b+\eta\,e$, onde $\eta>0$ é a taxa de aprendizado.
|
Frank Rosenblatt em 1960 conectando o Mark 1 Perceptron. Fonte: Perceptron Demo.
|
Perceptron em Pytorch¶
def set_device(on_gpu=True):
has_mps = torch.backends.mps.is_available()
has_cuda = torch.cuda.is_available()
return "mps" if (has_mps and on_gpu) \
else "cuda" if (has_cuda and on_gpu) \
else "cpu"
device = set_device(on_gpu=True)
class Perceptron():
def __init__(self, num_features):
self.num_features = num_features
self.weights = torch.zeros(
num_features, 1, dtype=torch.float32, device=device)
self.bias = torch.zeros(1, dtype=torch.float32, device=device)
self.ones = torch.ones(1, device=device)
self.zeros = torch.zeros(1, device=device)
def forward(self, x):
linear = torch.mm(x, self.weights) + self.bias
predictions = torch.where(linear > 0., self.ones, self.zeros)
return predictions
def backward(self, x, y):
predictions = self.forward(x)
errors = y - predictions
return errors
def train(self, x, y, epochs):
for _ in range(epochs):
for i in range(y.shape[0]):
errors = self.backward(
x[i].reshape(1, self.num_features), y[i]).reshape(-1)
self.weights += (errors * x[i]).reshape(self.num_features, 1)
self.bias += errors
def evaluate(self, x, y):
predictions = self.forward(x).reshape(-1)
accuracy = torch.sum(predictions == y).float() / y.shape[0]
return accuracy
Treinando o Modelo¶
ppn = Perceptron(num_features=2)
X_train_tensor = torch.tensor(
X_train,
dtype=torch.float32,
device=device)
y_train_tensor = torch.tensor(
y_train,
dtype=torch.float32,
device=device)
ppn.train(X_train_tensor, y_train_tensor, epochs=5)
print('Model parameters:')
print('\tWeights:', ppn.weights.tolist())
print('\tBias: ', ppn.bias.tolist())
Model parameters: Weights: [[-1.0376710891723633], [-1.455593466758728]] Bias: [0.0]
Avaliando o Modelo nos dados de Teste¶
X_test_tensor = torch.tensor(
X_test,
dtype=torch.float32,
device=device)
y_test_tensor = torch.tensor(
y_test,
dtype=torch.float32,
device=device)
test_acc = ppn.evaluate(X_test_tensor, y_test_tensor)
print(f'Test set accuracy: {(test_acc*100):.2f}%')
Test set accuracy: 96.67%
Visualizando a Fronteira de Decisão¶
Adaline: Adaptive Linear Neuron¶
|
Adaline. Image Source: Sebastian Raschka.
|
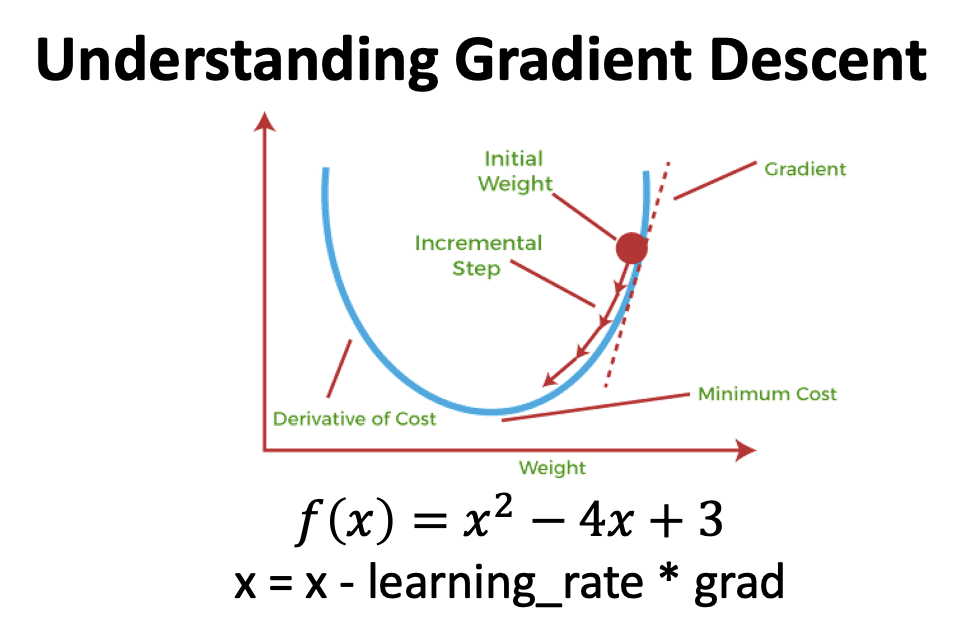
Gradiente Descendente¶
Atualização de parâmetros do modelo utilizando informação do gradiente de uma função de custo (loss) $\mathcal{L}(w,b)$: $\nabla(\mathcal{L}(w,b))$.
Ou seja, dar um passo na direção oposta do gradiente. $$\Delta w = - \eta \times \nabla_w(\mathcal{L}(w,b))$$ $$\Delta b = - \eta \times \nabla_b(\mathcal{L}(w,b))$$
- $\eta$: learning rate (tamanho do passo)
Gradiente da função de custo com respeito a $w_j$ e a $b$:
$$\frac{\partial \mathcal{L}}{\partial w_j} = - \frac{1}{m} \sum_i (y^i - \sigma(z^i))x^i_j$$$$\frac{\partial \mathcal{L}}{\partial b} = - \frac{1}{m} \sum_i (y^i - \sigma(z^i))$$Gradiente Descendente (cont.)¶
Podemos escrever a atualização de weights e bias como:
- $\Delta w_j = - \eta (\frac{\partial \mathcal{L}}{\partial w_j})$
- $\Delta b = - \eta (\frac{\partial \mathcal{L}}{\partial b)}$
Usamos um algoritmo para computar gradientes com base no conjunto completo de dados de treinamento e atualizar os parâmetros do modelo. Essa atualização se dá realizando um pequeno passo na direção oposta do gradiente da loss $\Delta \mathcal{L}(w,b)$.
Limitação do Perceptron¶
Mas e quanto à porta XOR?
Perceptron: Limitações¶
|
Limitação do Perceptron. Image Source: Sebastian Raschka.
|
Funções de Ativação (Não-lineares)¶
|
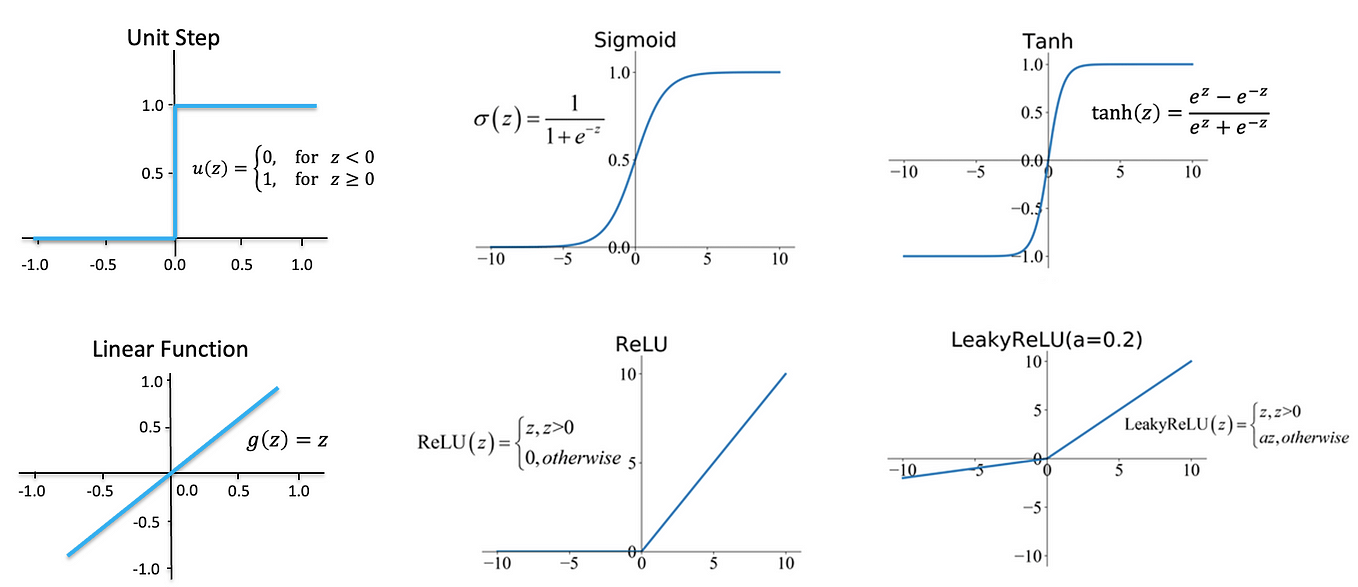Funções de Ativação. Fonte: Prazan NH.
|
MLP: Demo Visual¶
Redes Neurais: Empilhando Perceptrons¶
- Multilayer Perceptron (MLP)
- Noção de camada (layer): operações parametrizadas sobre tensores.
- Conceito de arquitetura: Camada de entrada, várias camadas escondidas, uma cada de saída.
MLP: Treinamento¶
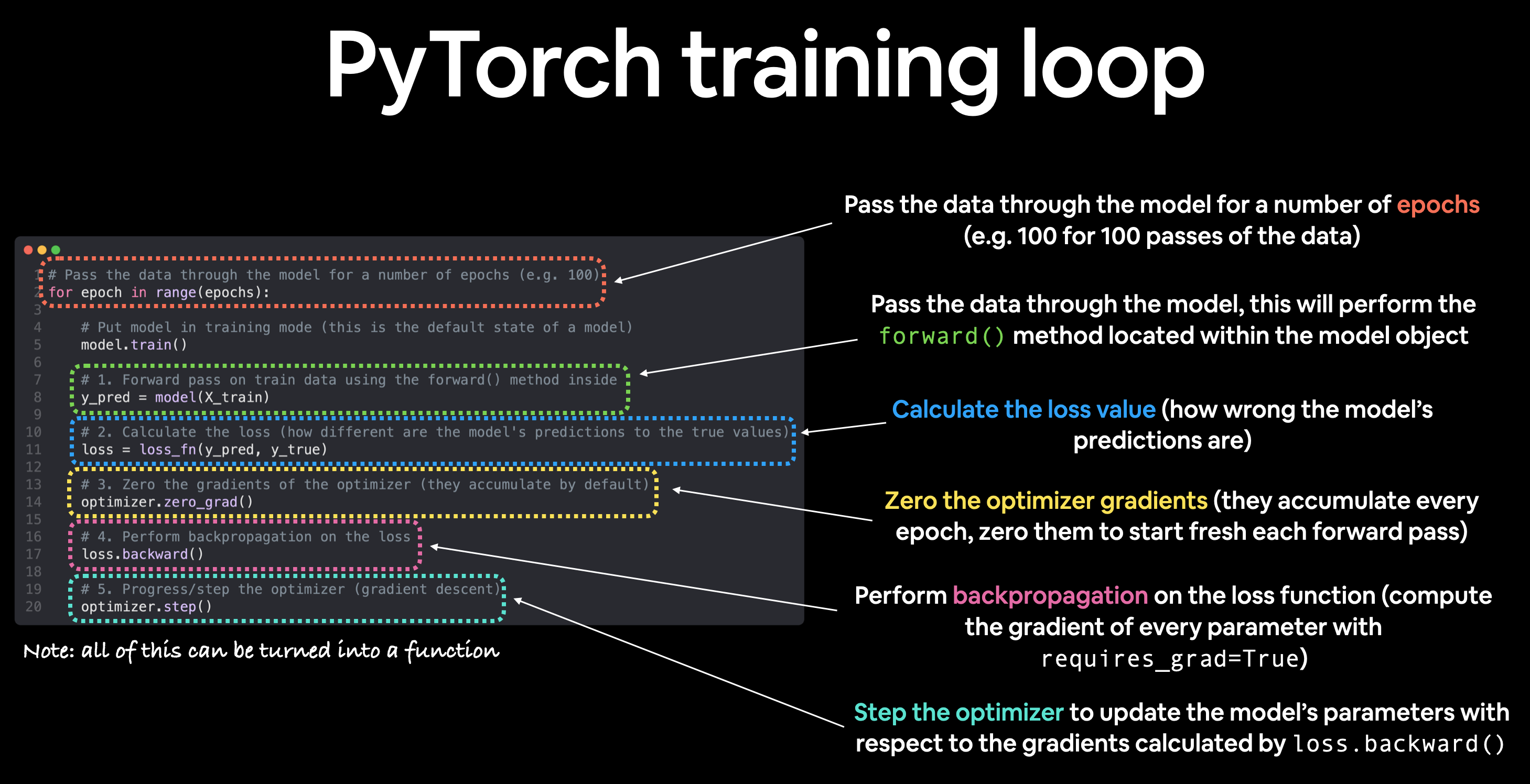
O procedimento de treinamento do MLP pode ser resumido em três etapas simples:
- A partir da camada de entrada, propagamos adiante ("feed‑forward") os padrões dos dados de treinamento através da rede para gerar uma saída.
- Com base na saída da rede, calculamos a perda (loss) que queremos minimizar usando uma função de perda que descreveremos mais adiante.
- Propagamos a loss para trás (back‑propagation), determinamos sua derivada em relação a cada peso e viés da rede, e atualizamos o modelo.
Por fim, após repetirmos essas três etapas por múltiplas épocas e aprendermos os parâmetros de peso e viés do MLP, usamos a propagação adiante para calcular a saída da rede e aplicamos uma função de limiar (threshold) para obter as classes previstas.
MLP: Feed-forward¶
Vamos analisar passo a passo a propagação adiante para gerar uma saída a partir dos padrões presentes nos dados de treinamento. Como cada unidade da camada oculta está conectada a todas as unidades das camadas de entrada, primeiro calculamos a unidade de ativação da camada oculta $a_1^{(h)}$ da seguinte forma:
$$ z_1^{(h)} = x_1^{(\text{in})}w_{1,1}^{(h)} + x_2^{(\text{in})}w_{1,2}^{(h)} + \ldots + x_m^{(\text{in})}w_{1,m}^{(h)} $$$$ a_1^{(h)} = \sigma(z_1^{(h)}) $$Aqui, $z_1^{(h)}$ é a entrada líquida (net input) e $\sigma(.)$ é a função de ativação, que deve ser diferenciável para permitir o aprendizado dos pesos que conectam os neurônios por meio de uma abordagem baseada em gradiente. Para resolver problemas complexos, como classificação de imagens, precisamos de funções de ativação não lineares no nosso modelo MLP; um exemplo comum é a função sigmoide (logística):
$$ \sigma(z) = \frac{1}{1 + e^{-z}} $$A função sigmoide é uma curva em forma de S que mapeia a entrada líquida $z$ para uma distribuição logística no intervalo de 0 a 1, cruzando o eixo $y$ quando $z = 0$.
MLP: Feed-Forward (cont.)¶
Escrevemos a ativação em uma forma mais compacta e vetorizada (para evitar loops): $$ z^{(h)} = x^{(\text{in})}W^{(h)T} + b^{(h)} $$
$$ a^{(h)} = \sigma(z^{(h)}) $$Aqui, $x^{(\text{in})}$ é o nosso vetor de características de dimensão $1\times m$.
$W^{(h)}$ é uma matriz de pesos de dimensão $d\times m$, onde $d$ representa o número de unidades na camada oculta; consequentemente, a matriz transposta $W^{(h)T}$ tem dimensão $m\times d$.
O vetor de viés $b^{(h)}$ contém $d$ unidades de bias (uma para cada nó oculto).
Após a multiplicação matricial‑vetorial, obtemos o vetor de entrada líquida $\;z^{(h)}\;$ de dimensão $1\times d$, que será usado para calcular a ativação $a^{(h)} \in \mathbb{R}^{1\times d}$.
MLP: Feed-Forward (cont.)¶
Podemos generalizar este cálculo para os $n$ exemplos do conjunto de treinamento:
$$ Z^{(h)} = X^{(\text{in})}W^{(h)T} + b^{(h)} $$Neste caso, $X^{(\text{in})}$ passa a ser uma matriz $n\times m$; a multiplicação matricial resulta em uma matriz de entrada líquida $\;Z^{(h)}\;$ de dimensão $n\times d$. Por fim, aplicamos a função de ativação $\sigma(\cdot)$ a cada elemento da matriz de entrada líquida para obter a matriz de ativação $n\times d$ na camada seguinte (aqui, a camada de saída):
$$ A^{(h)} = \sigma(Z^{(h)}) $$De maneira análoga, podemos escrever a ativação da camada de saída em forma vetorizada para múltiplos exemplos:
$$ Z^{(\text{out})} = A^{(h)}W^{(\text{out})T} + b^{(\text{out})} $$Aqui multiplicamos a transposta da matriz $t\times d$ $W^{(\text{out})}$ (onde $t$ é o número de unidades de saída) pela matriz $n\times d$ $A^{(h)}$, e somamos o vetor de viés de dimensão $t$, $b^{(\text{out})}$, obtendo a matriz $Z^{(\text{out})}$ de dimensão $n\times t$. (As linhas desta matriz representam as saídas para cada exemplo.)
Por fim, aplicamos a função sigmoide para obter o valor contínuo da saída do nosso modelo:
$$ A^{(\text{out})} = \sigma(Z^{(\text{out})}) $$Componentes de uma Rede Neural¶
- Arquitetura: Camadas, parâmetros, neurônios e conexões
- Função de ativação
- Função de custo/perda (loss)
- Otimizador
MLP para Classificação de Imagens¶
Vamos construir e treinar uma MLP para classificar imagens de dígitos escritos à mão presentes no dataset Mixed National Institute of Standards and Technology (MNIST), construído por Yann LeCun e colaboradores, publicado em 1998 (Gradient-Based Learning Applied to Document Recognition).
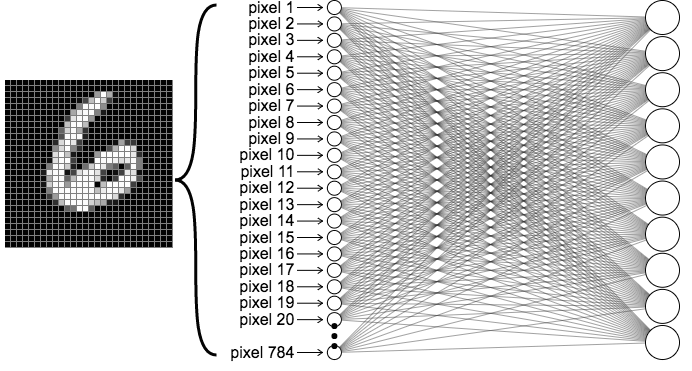
MNIST dataset. Dígitos são imagens de 28x28 pixels (ou seja, 784 dimensões). Fonte: Wikipedia.
|
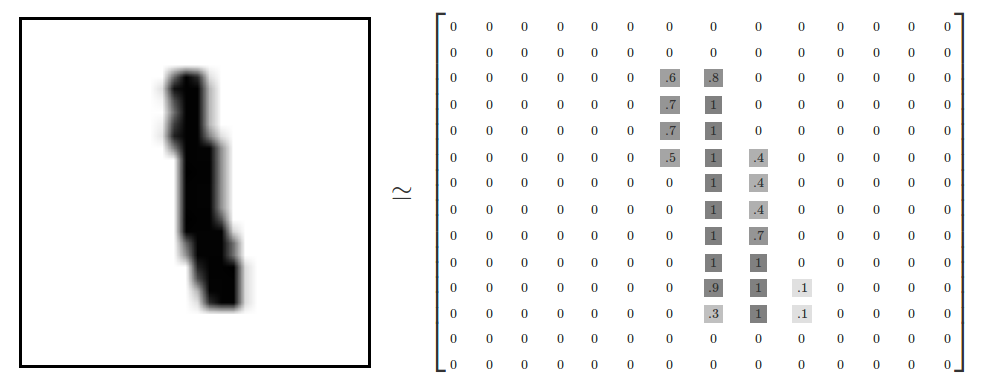Exemplo de dígito 1 no MNIST dataset. Fonte: Tensorflow.
|
MLP MNIST: Tutorial Visual (YouTube)¶
from IPython.display import YouTubeVideo
YouTubeVideo("aircAruvnKk", width=600, height=350)
MLP e MNIST em Pytorch¶
from torchvision import datasets
import torchvision.transforms as transforms
import torch.utils.data as data
# Número de processos para o dataloader
NUM_WORKERS = 0
# Quantas amostras (imagens) por batch
BATCH_SIZE = 128
# Converte dados em tensores
transform = transforms.ToTensor()
# Carrega dados de treino e teste
train_data = datasets.MNIST(root='data', train=True,
download=True, transform=transform)
test_data = datasets.MNIST(root='data', train=False,
download=True, transform=transform)
# Cria dataset de validação
VALIDATION_SIZE = 0.1
n_train_examples = int(len(train_data) * VALIDATION_SIZE)
n_valid_examples = len(train_data) - n_train_examples
train_data, valid_data = data.random_split(
train_data, [n_train_examples, n_valid_examples])
# Data Loaders
train_loader = torch.utils.data.DataLoader(train_data, shuffle=True,
batch_size=BATCH_SIZE, num_workers=NUM_WORKERS)
valid_loader = torch.utils.data.DataLoader(valid_data,
batch_size=BATCH_SIZE, num_workers=NUM_WORKERS)
test_loader = torch.utils.data.DataLoader(test_data,
batch_size=BATCH_SIZE, num_workers=NUM_WORKERS)
Arquitetura da Rede Neural¶
import torch.nn as nn
import torch.nn.functional as F
class MLPNet(nn.Module):
def __init__(self):
super(MLPNet, self).__init__()
self.flatten = nn.Flatten()
# input layer
self.fc1 = nn.Linear(28 * 28, 64)
# linear layer (n_hidden -> hidden_2)
self.fc2 = nn.Linear(64, 32)
# linear layer (n_hidden -> 10)
self.fc3 = nn.Linear(32, 10)
def forward(self, x):
x = self.flatten(x)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
Função de Custo/Loss para Classificação¶
- Cross‑Entropy Loss: $\mathcal{L}(\mathbf{y},\hat{\mathbf{y}})= -\sum_{k=1}^{K} y_k\,\log(\hat y_k)$
- Intuição
- Mede a divergência entre o vetor de rótulos reais $y$ (ou $y_k$) e a distribuição predita $\hat{y}$.
- Penaliza fortemente previsões que atribuem baixa probabilidade ao verdadeiro rótulo.
- Propriedades importantes
- Não‑negatividade: $\mathcal{L} \ge 0$; zero apenas quando $\hat y = y$.
- Derivada simples: facilita a implementação do algoritmo de backpropagation.
- Quando usar: Binária ou multiclasse quando as saídas são interpretadas como probabilidades (softmax ou sigmoid).
import torch.optim as optim
EPOCHS = 10
device = set_device(on_gpu=True)
model = MLPNet().to(device)
loss_function = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.02)
num_parameters = sum(p.numel() for p in model.parameters() if p.requires_grad)
print(f"Num. Parâmetros no modelo:", num_parameters)
Num. Parâmetros no modelo: 52650
from IPython.display import YouTubeVideo
YouTubeVideo("Nutpusq_AFw", width=600, height=350)
epoch_ticks = [i+1 for i in range(EPOCHS)]
plt.figure(figsize=(4,3))
plt.plot(epoch_ticks, tr_loss, "-o", label="Train. Loss")
plt.plot(epoch_ticks, val_loss, "--^", label="Valid. Loss")
plt.xlabel('Epoch')
plt.xlabel('Loss')
plt.title("Comportamento da Loss")
plt.legend(loc='lower left', fontsize=8)
plt.show()
Testando o Modelo¶
- Avaliar se o modelo generaliza bem para dados que não foram vistos pela rede durante o treinamento (unseen data).
- Importante: usar
model.eval()para configurar o modelo em evaluation mode.
def get_predictions(model, iterator, device):
model.eval()
images, labels, probs = [], [], []
with torch.no_grad():
for (x, y) in iterator:
x = x.view(-1, 28*28).to(device)
y = y.to(device)
y_pred = model(x)
y_prob = F.softmax(y_pred, dim=-1)
images.append(x.cpu())
labels.append(y.cpu())
probs.append(y_prob.cpu())
images = torch.cat(images, dim=0)
labels = torch.cat(labels, dim=0)
probs = torch.cat(probs, dim=0)
return images, labels, probs
Função de Ativação na Camada de Saída¶
- Camada de Saída com Softmax: Cabeça de Classificação (Classification Head)
- Propósito principal: Converter vetores de logits (saída da última camada escondida) $z \in \mathbb{R}^{K}$ em uma distribuição de probabilidade sobre $K$ classes.
- Definição matemática: $\sigma(z)_k = \frac{\exp(z_k)}{\sum_{j=1}^{K} \exp(z_j)}, \qquad k=1,\dots ,K$
- Cada componente fica no intervalo $(0,1)$ e a soma totaliza $1$.
- Derivada simples: $ \frac{\partial \sigma(z)_i}{\partial z_j} = \sigma(z)_i (\delta_{ij} - \sigma(z)_j)$, onde $\delta_{ij}$ é a função indicadora.
- Junto com a loss Cross‑Entropy, forma o padrão ouro “Softmax + Cross‑Entropy”.
Função Softmax para classificação. Fonte: Abhisek Jana.
images, labels, probs = get_predictions(model, test_loader, device)
pred_labels = torch.argmax(probs, 1)
import sklearn.metrics as mtr
import seaborn as sns
fig = plt.figure(figsize=(7, 5))
ax = fig.add_subplot(1, 1, 1)
cm = mtr.confusion_matrix(labels, pred_labels)
sns.heatmap(
cm, annot=True, fmt='d', cmap='bone_r', cbar=False,
square=True, linewidths=3, linecolor="w", ax=ax)
plt.show()
import numpy as np
dataiter = iter(test_loader)
images, labels = next(dataiter)
images = images.view(-1, 28*28).to(device)
labels = labels.to(device)
output = model(images)
_, preds = torch.max(output, 1)
images = images.cpu()
fig = plt.figure(figsize=(3, 3))
for idx in np.arange(20):
ax = fig.add_subplot(4, int(20/4), idx+1, xticks=[], yticks=[])
ax.imshow(images[idx].view(28,28), cmap='gray')
ax.set_title("{} ({})".format(str(preds[idx].item()), str(labels[idx].item())),
color=("green" if preds[idx]==labels[idx] else "red"))
plt.tight_layout()
plt.show()
Salvando o modelo¶
torch.save(model.state_dict(), "mlp-mnist-model.pth")
Carregando o modelo¶
model = MLPNet()
model.load_state_dict(torch.load("mlp-mnist-model.pth"))
model.eval();
Resumo¶
|
Leitura Recomendada: Capítulo 6.
|