Visão Computacional¶
Redes Neurais Convolucionais (CNNs)¶
Prof. Dr. Denis Mayr Lima Martins¶
Pontifícia Universidade Católica de Campinas¶
Limitações da Rede MLP¶
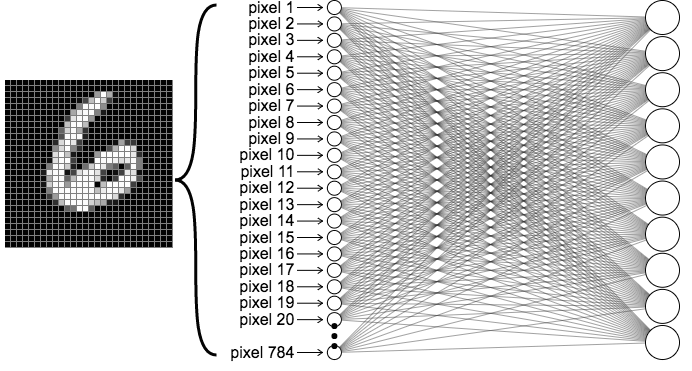
- Dimensionalidade Alta: Uma imagem 224x244x3 tem 150.528 pixels/entradas. Cada neurônio na primeira camada oculta de um MLP precisaria de 150.528 pesos, levando a bilhões de parâmetros treináveis em uma rede profunda.
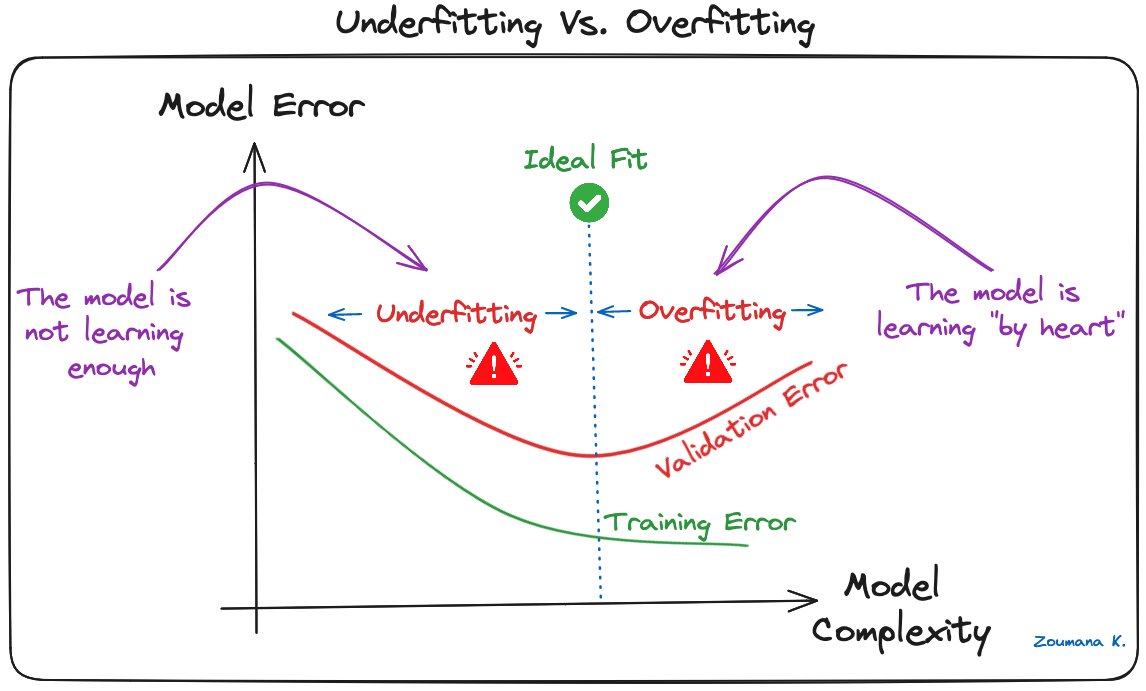
- O grande número de parâmetros torna o modelo propenso a overfitting (superajuste).
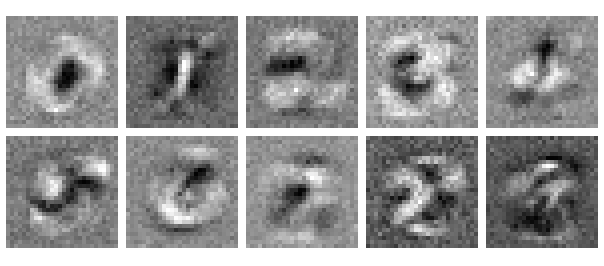
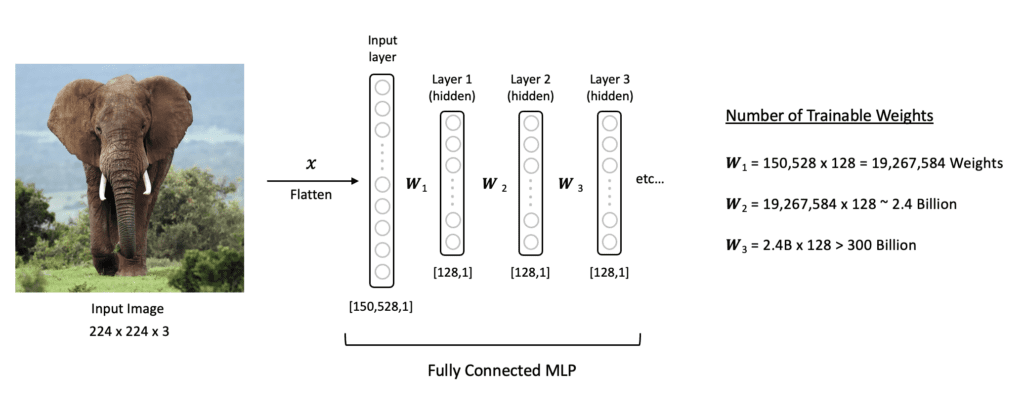Alta dimensionalidade das MLPs para imagens. Frequentemente levando a overfitting. Fonte: LearnOpenCV.
Limitações da Rede MLP¶
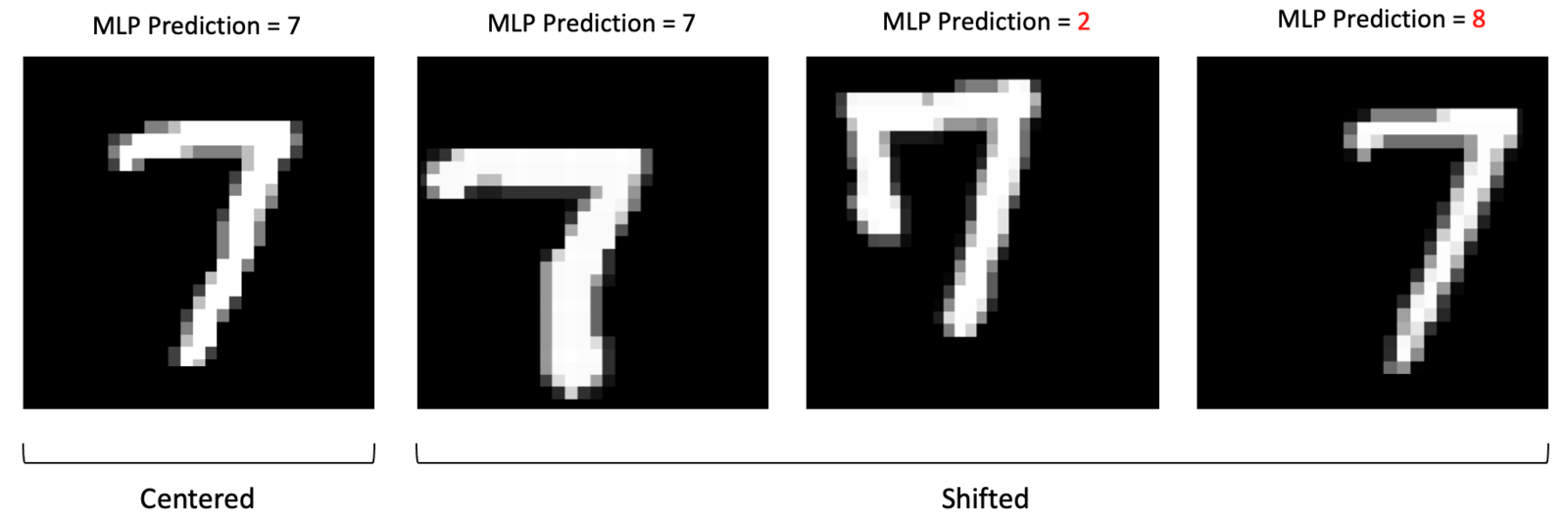
- Perda de Estrutura Espacial: MLPs exigem que a imagem 2D/3D seja "achatada" (flattened) em um vetor 1D.
- Isso destrói a informação de localidade: pixels próximos (semânticos) são tratados da mesma forma que pixels distantes.
Objetivos de Aprendizagem¶
- Explicar por que CNNs são adequadas para dados de imagem.
- Descrever os blocos fundamentais (convolução, padding, stride, pooling, ativação).
- Esboçar uma arquitetura simples de CNN e justificar cada componente.
- Implementar um CNN mínimo em PyTorch que classifica dígitos MNIST.
Redes Neurais Convolucionais¶
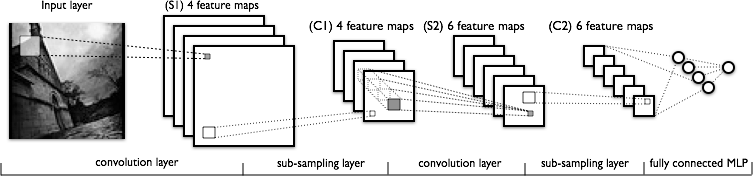
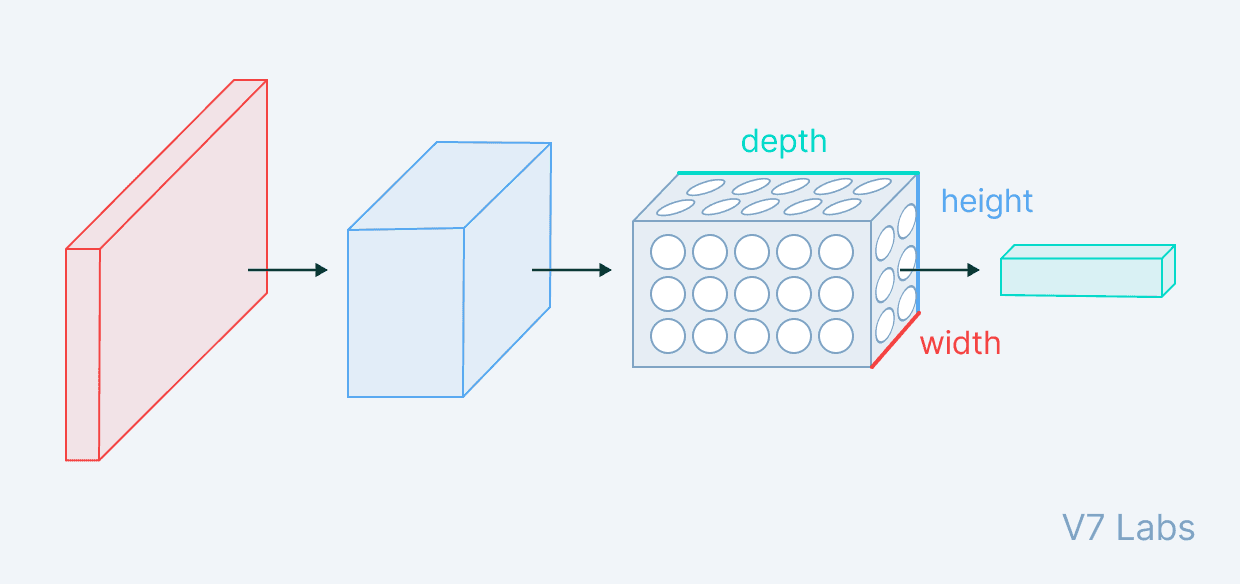
- Convolutional Neural Nets (CNNs ou ConvNets) são arquiteturas de redes neurais otimizadas para dados com estrutura de grade, como imagens.
- CNN aplica uma série de transformações na imagem original (veja esquema abaixo) com três tipos de camadas (convolution, pooling e fully connected).
- A sequência de camadas antes da camada fully connected é chamada de extrator de características.
In [1]:
import torch.nn as nn
import torch.nn.functional as F
class SimpleCNN(nn.Module):
def __init__(self):
super(SimpleCNN, self).__init__()
self.sequential = nn.Sequential(
# Primeira camada convolucional
nn.Conv2d(in_channels=1, out_channels=32,
kernel_size=2, padding=1),
nn.ReLU(),
# Segunda camada convolucional
nn.Conv2d(in_channels=32, out_channels=64,
kernel_size=2, padding=1),
# Pooling Max: 2x2
nn.MaxPool2d(kernel_size=2, stride=2),
# Flatten de matriz para vetor.
nn.Flatten(),
# Definindo as camadas FC
# Camada Totalmente Conectada 1
nn.Linear(14400, 128),
nn.ReLU(),
# Camada de Saída (10 classes para MNIST)
nn.Linear(128, 10)
)
def forward(self, x):
return self.sequential(x)
In [7]:
train_model_mini_batch_with_validation(
EPOCHS,
train_loader,
valid_loader,
model,
loss_function,
optimizer)
Training: 0%| | 0/10 [00:00<?, ?it/s]
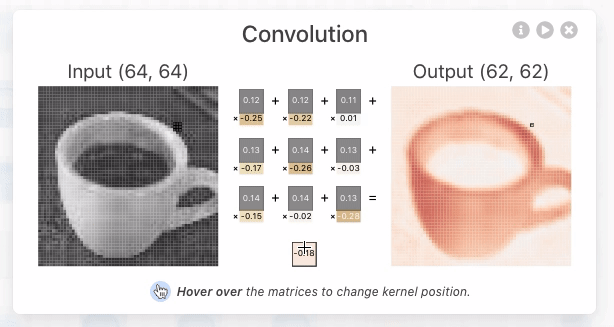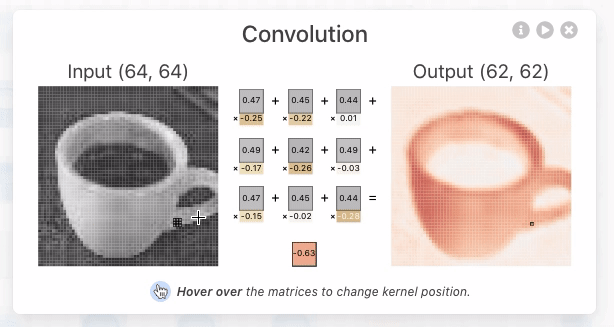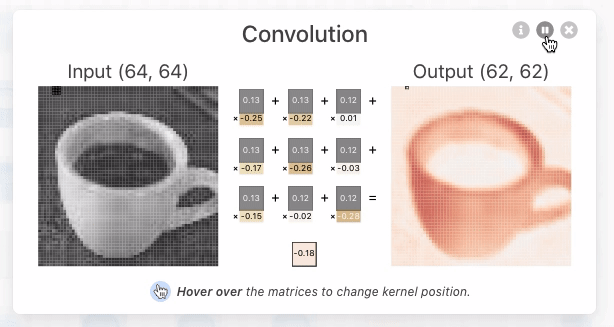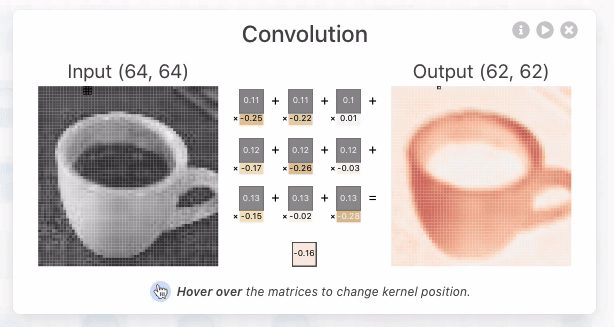
Convolução em CNNs¶
|
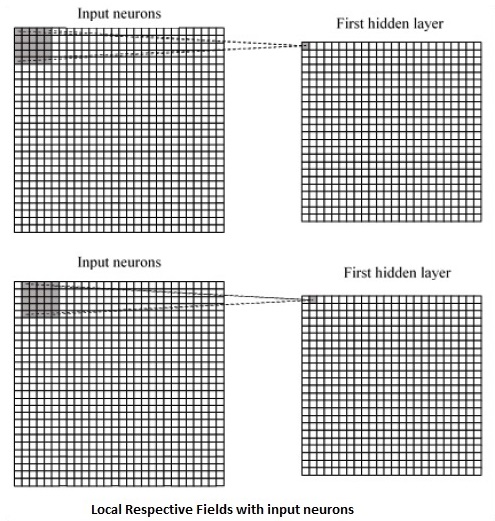Convolução na camada escondida. Fonte: Michael Nielsen.
|
Convolução em CNNs¶
|
Convolução no primeiro neurônio da camada escondida. Fonte: Michael Nielsen.
|
Convolução em CNNs¶
- A operação de convolução (para fins de CNN) é o produto escalar (multiplicação elemento a elemento seguida por soma) entre o filtro e a região de entrada correspondente. $\text{Output} = \sum_{i, j} (\text{Input}_{i, j} \times \text{Filter}_{i, j}) + \text{Bias} $
- O resultado é um único número que mede o grau de correspondência do filtro com a região de entrada. Veja também: Convolution arithmetic.
- Esse processo é repetido para cada localização onde o filtro desliza.
- Os resultados são colocados em uma matriz de saída chamada Mapa de Ativação (Activation Map) ou Mapa de Características (Feature Map).
Hyperparâmetros da Convolução¶
- Kernel Size ($F$): Tamanhos comuns são $3 \times 3$ ou $5 \times 5$. Tamanhos menores são frequentemente preferidos para extrair features com menos parâmetros.
- Número de Filtros: Aumenta com a profundidade; geralmente começa em 32 e dobra (64, 128, etc.).
- Stride ($S$): É o número de pixels que o filtro se move (desloca) sobre a entrada a cada iteração.
- Stride = 1: O filtro se move um pixel por vez, resultando em sobreposição de campos receptivos e um mapa de ativação grande.
- Stride > 1: Causa um "salto" maior do filtro, resultando em menos etapas e um mapa de ativação espacialmente menor.
- Um stride maior reduz a dimensionalidade e o custo computacional.
- Padding: É a adição de pixels extras (geralmente com valor zero, Zero-Padding) em torno das bordas da imagem de entrada.
- Problema de Redução: Sem padding, a convolução geralmente reduz o tamanho espacial da saída. Padding garante que os pixels de borda (que seriam pouco usados) participem do campo receptivo.
- Padding "Same" (Igual): Adiciona zeros o suficiente para que a dimensão espacial da saída seja a mesma da entrada (assumindo $S=1$).
- Padding "Valid" (Válido): Não usa padding, resultando em uma saída menor que a entrada.
Mapa de Ativação¶
Determinando o Tamanho do Mapa de Ativação:
- O tamanho espacial de saída $O$ de uma camada convolucional é determinado pela dimensão de entrada ($N$), tamanho do kernel ($F$), Padding ($P$) e Stride ($S$).
- Para que o resultado seja um inteiro, a fórmula abaixo deve ser satisfeita.
Exemplo: Imagem de entrada $32 \times 32$ ($N=32$), Kernel $5 \times 5$ ($F=5$).
- Cenário 1 (Stride e Padding): Stride $S=1$. Para obter Same Padding (preservar 32x32), $P$ deve ser: $P = (F-1)/2 = (5-1)/2 = 2$.
- $O = \frac{32 - 5 + 2(2)}{1} + 1 = \frac{31}{1} + 1 = 32$
- A saída é $32 \times 32$ (tamanho preservado).
- Cenário 2 (Sem Padding, Stride 1): $P=0, S=1$.
- $O = \frac{32 - 5 + 0}{1} + 1 = 27 + 1 = 28 $
- A saída é $28 \times 28$.
Compartilhamento de Parâmetros¶
- O Compartilhamento de Parâmetros é uma característica distintiva das CNNs.
- O mesmo filtro (conjunto de pesos) é usado em todas as posições espaciais da camada de entrada.
- Para um filtro 5x5: $\sigma\left(b + \sum_{l=0}^4 \sum_{m=0}^4 w_{l,m} a_{j+l, k+m} \right)$
- Vantagem I: Redução de Parâmetros: Em vez de cada neurônio ter seu próprio conjunto de pesos, muitos neurônios compartilham o mesmo filtro.
- Vantagem II: Equivariância à Translação: Se uma característica (ex: uma linha) for útil em uma parte da imagem, ela será útil em qualquer outra parte.
- O filtro aprende a detectar a característica independentemente da sua localização exata.
Função de Ativação (ReLU)¶
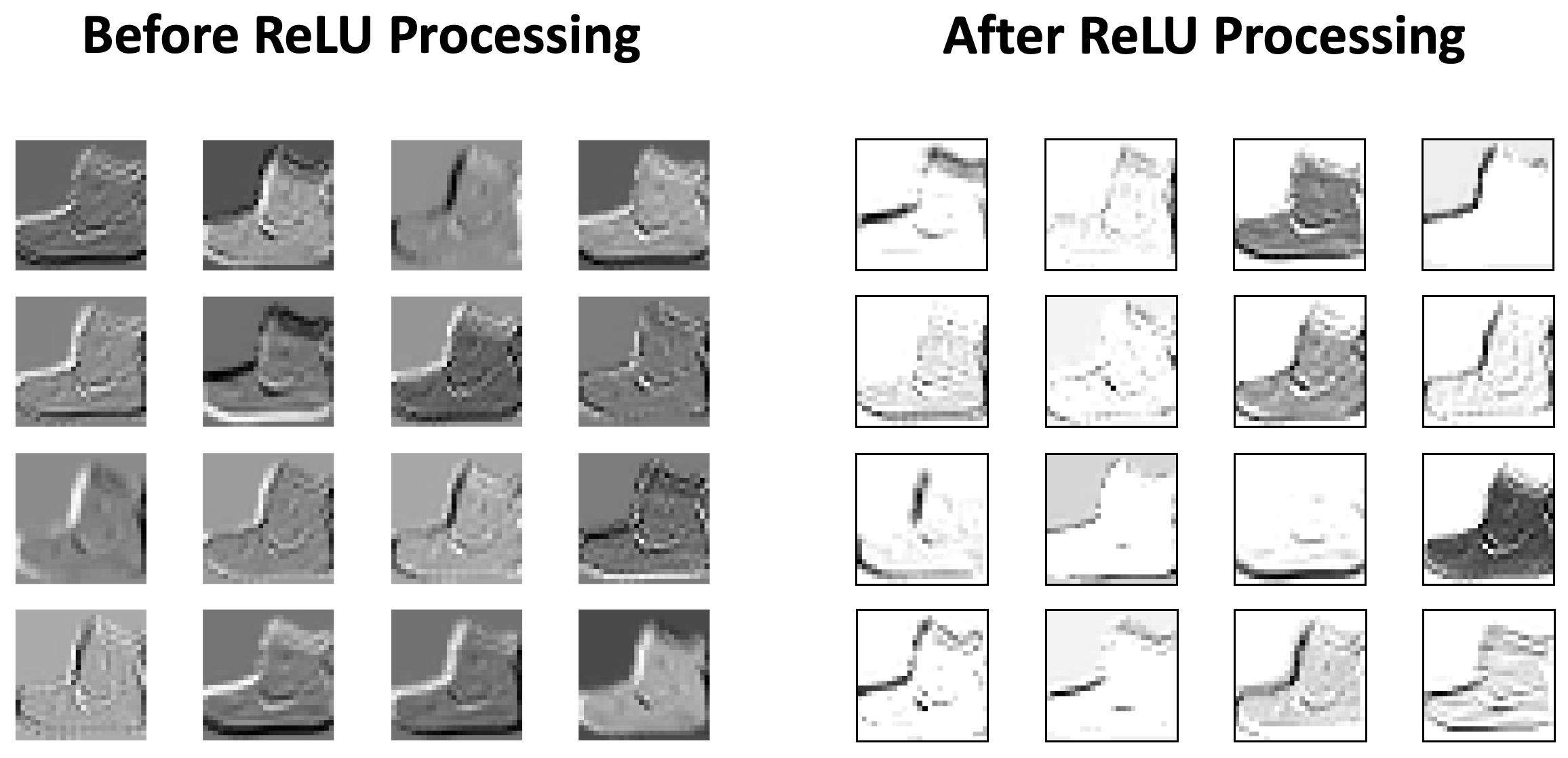
- Após a operação de convolução (que é linear), uma função de ativação é aplicada ao mapa de ativação para introduzir não-linearidade.
- ReLU é a função mais comum: $f(x) = \max(0, x)$.
- Ela remove valores negativos, ajustando-os para zero, o que pode ser visto como uma função de limiar (thresholding).
Pooling (Subamostragem)¶
- O Pooling é uma forma de subamostragem (downsampling) não linear, geralmente inserida periodicamente entre camadas convolucionais.
- Objetivos Principais:
- Reduzir a dimensionalidade espacial (Altura e Largura).
- Reduzir o número de parâmetros e a quantidade de computação.
- Ajudar a controlar o overfitting.
- Conceder um grau de invariância local à translação.
- O filtro de pooling não tem parâmetros treináveis (não tem pesos).
- Um $2 \times 2$ Max Pooling com $S=2$ descarta 75% das ativações espaciais
Max pooling. Fonte: Stanford.edu.
|
Average pooling. Fonte: Stanford.edu.
|
Fully Connected (FC)¶
- Após uma série de camadas Convolucionais e de Pooling, o volume de dados contém características de alto nível.
- A última etapa é a classificação, realizada por camadas Totalmente Conectadas (FC) (ou densas).
- Flattening (Achatamento): O volume 3D final do extrator de características deve ser convertido em um vetor 1D antes de entrar na primeira camada FC.
- As camadas FC mapeiam as características extraídas para as probabilidades de classe.
- O número de neurônios na camada de saída é igual ao número de classes (e.g., 10 para MNIST).
- Para classificação de imagens: A camada de saída do classificador FC tipicamente usa a função de ativação Softmax para converter os valores brutos de saída da rede em probabilidades normalizadas.
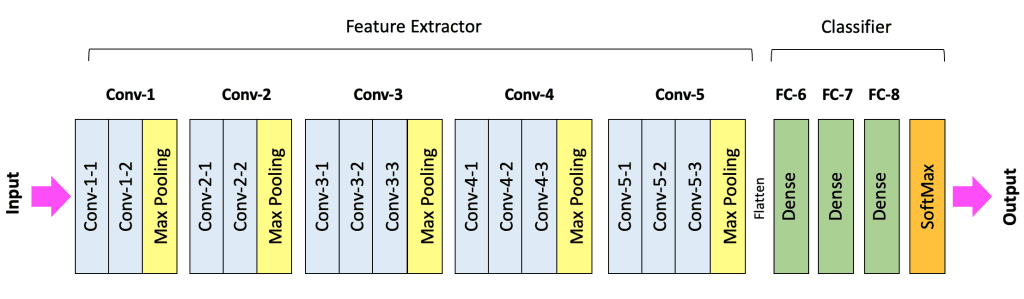
Arquitetura CNN¶
- Uma CNN de classificação é dividida em duas partes principais:
- Extrator de Características (Feature Extractor): Composto por blocos Conv + ReLU + Pooling (ou ConvBlocks). É comum empilhar 2 ou 3 camadas Conv/ReLU consecutivas antes de uma camada Pooling.
- Classificador (Classifier): Composto por camadas FC + Softmax.
- O fluxo de dados transforma o volume de entrada, tipicamente reduzindo as dimensões espaciais (H, W) e aumentando a profundidade (Canais/Filtros).
- Hierarquia de Características:
- Camadas iniciais aprendem elementos simples (bordas, cores).
- Camadas médias combinam elementos simples em formas mais complexas (e.g., olhos, rodas).
- Camadas profundas aprendem conceitos abstratos de alto nível (e.g., faces, objetos inteiros).
Treinamento¶
- As CNNs são tipicamente treinadas usando Aprendizado Supervisionado.
- Os pesos iniciais (elementos dos filtros) são definidos aleatoriamente.
- O processo de aprendizagem utiliza o Backpropagation e o Gradiente Descendente.
- Loss Function (Função de Perda): Mede o erro entre a previsão da rede e o rótulo verdadeiro (Ground Truth).
- Otimização: O algoritmo ajusta iterativamente os pesos (filtros e FC) para minimizar a perda.
Mais informações sobre o algoritmo de Backpropagation e Gradiente Descendente na próxima aula.
Resumo¶
|
Leitura Recomendada: Capítulo 9.
|
Perguntas e Discussão¶
- O Perceptron Multicamadas (MLP) é a arquitetura básica de redes neurais. Por que os MLPs são inerentemente inadequados para processar imagens de alta resolução, e como a CNN supera a principal limitação de dimensionalidade do MLP?
- As três principais operações em um extrator de características de CNN são Convolução, ReLU e Pooling. Qual é a contribuição fundamental de cada uma dessas operações para a capacidade de uma CNN aprender e generalizar, especialmente no contexto de downsampling?
- O treinamento de uma CNN envolve o aprendizado automático de filtros (pesos). Descreva a natureza hierárquica das características aprendidas em CNNs profundas. O que um filtro (kernel) típico nas camadas iniciais detecta em comparação com as características detectadas nas camadas mais profundas?
- Qual é o objetivo do Zero-Padding e qual o valor de padding ($P$) deve ser escolhido para um filtro de tamanho $F$ se quisermos garantir que a saída espacial ($O$) seja exatamente a mesma que a entrada espacial ($N$), assumindo um Stride ($S$) de 1? Demonstre usando a fórmula do tamanho de saída.
- Vimos que os filtros não são pré-definidos manualmente, mas sim aprendidos. Na fase de treinamento, como o algoritmo de Backpropagation (Retropropagação) "sabe" qual filtro deve ser ajustado para detectar uma curva ou uma linha, se os pesos são inicializados aleatoriamente? Por que esse processo não é considerado "sorte" ou aleatório?